math weakness essay

Reach More Learners
Learning Framework
Our Philosophy
A Note to Parents and Other Caregivers
Our Online Modules
Professional Development
Learning Library
Case Studies
Connections with Other Initiatives
Schools for All Kinds of Minds – About the Book
Schools for All Kinds of Minds – Using the Book
Schools for All Kinds of Minds – Meet the Authors
Schools for All Kinds of Minds – See What People are Saying
Buy the Book

Mathematics Difficulties

Home — Essay Samples — Psychology — Personal Development Planning — My Academic Strengths And Academic Weaknesses

My Academic Strengths and Academic Weaknesses

Categories: Personal Development Planning

About this sample

Words: 530 |

Published: Aug 1, 2024

Words: 530 | Page: 1 | 3 min read

Cite this Essay

To export a reference to this article please select a referencing style below:

Let us write you an essay from scratch

450+ experts on 30 subjects ready to help
Custom essay delivered in as few as 3 hours

Get high-quality help

Prof Ernest (PhD)

Verified writer

Expert in: Psychology

+ 120 experts online

By clicking “Check Writers’ Offers”, you agree to our terms of service and privacy policy . We’ll occasionally send you promo and account related email

No need to pay just yet!

Related Essays

5 pages / 2444 words

1 pages / 490 words

1 pages / 519 words

2 pages / 822 words

Remember! This is just a sample.

You can get your custom paper by one of our expert writers.

121 writers online

Still can’t find what you need?

Browse our vast selection of original essay samples, each expertly formatted and styled

Related Essays on Personal Development Planning

Help.open.ac.uk. (2019). Friends and family: When study gets difficult - Help Centre - Open University. Available at: Jou

Leadership development plays a crucial role in the professional and personal growth of individuals. Effective leadership is essential for driving organizational success, inspiring teams, and fostering innovation. Moreover, [...]

My practicum experience has been an eye-opening and enriching journey that has allowed me to apply the knowledge and skills I have learned in the classroom to a real-world setting. The opportunity to work in a professional [...]

The Last Lecture, a book co-authored by Randy Pausch and Jeffrey Zaslow, is a memoir based on the final lecture delivered by Randy Pausch, a computer science professor at Carnegie Mellon University. The book provides valuable [...]

The first step in the development plan is to conduct a self-analysis such as SWOT and then identify the priority areas that junior managers need to become senior managers in the same organization. After completing this section, [...]

The protagonist of the book is William Kamkwamba. When the book begins, William is a firm believer in magic and has many superstitions. Though as the book progresses, he educates himself and nurtures his curiosity for science. [...]

Get Your Personalized Essay in 3 Hours or Less!

We use cookies to personalyze your web-site experience. By continuing we’ll assume you board with our cookie policy .

Instructions Followed To The Letter
Deadlines Met At Every Stage
Unique And Plagiarism Free

Become a Tutor
Find a Tutor
Previous Post

The Top 5 Reasons Students Struggle with Math

Why is math so hard? Take a look at the most common reasons why math is hard for students

Mathematics is often considered to be one of the most challenging subjects for students. Recent surveys report that 37% of teens aged 13-17 found math to be harder than other subjects – the highest ranked overall. So, if you’re out there wondering, “why do I struggle with math so much?” there may be a number of reasons, from attention difficulties to learning gaps from past math classes or even just lack of practice. Take a look at common reasons students struggle with math, and how to find the right help you need to succeed.

Contact your nearest Tutor Doctor to find a math tutor near you

1) attention difficulties.

One reason why math is hard to understand is because it often involves multi-step problems, and students need to be able to perform several consecutive steps to find a solution. This requires staying actively focused on the task at hand. When complex math procedures are being taught, students often lose focus and become distracted during the lesson. As a result, he or she may miss important steps in the problem-solving process, and later struggle with math when trying to complete problems on their own. Being able to revisit prior concepts that were previously unclear is one of the main benefits of Tutor Doctor’s individualized approach towards learning.

2) Math always builds upon previous concepts

Math is built on sequential learning. If a student didn’t fully understand a previous lesson’s concept, they are likely to struggle when newer concepts are introduced. To reduce fractions, students need to know division first; to do algebra, students need to be comfortable with multi-step arithmetic, and so on. Unfortunately, many students who are struggling with math feel uncomfortable or embarrassed asking questions in class when their teacher has already moved on to the next lesson. Math concepts are like building blocks, and the foundation always needs to be laid before moving forward. If the foundation isn’t there, the student will struggle in class and may not fully realize why they are struggling with math when their peers seem to be progressing along.

3) Concepts are learned, but not understood

Often times students know how to perform an operation from repetition, but don’t really understand the meaning behind it. For example, times-table memorization has always been a staple of elementary school curriculum. However, a student may only know that “4 x 4 = 16” because he or she memorized it, and not because they fully understand the concept of multiplication. For this reason, many students benefit from visual representations, such as using small objects (like marbles or paperclips) when learning multiplication and division. The fact is, all students learn differently, and it can be hard to encompass every student’s unique learning style in a classroom. That’s where individualized tutoring can really help those who struggle with math!

4) Lack of practice or patience

Many students simply don’t spend enough time practicing math concepts. Other students may not realize they need more time reviewing certain areas. Sometimes a student will feel like they understand a concept, but when attempting to do a problem themselves, they don’t know how to begin (or end up struggling through the process). Students will often feel confident after watching their teacher explain the lesson in class, only to find that doing it independently can be a lot more challenging. There’s unfortunately no quick and easy solution to learn math – it requires lots of practice and patience! As tutors, we try to specifically identify the areas in which students need improvement and focus on closing these “gaps” in learning.

5) “When am I ever going to use this?”

This classic line is a favorite of every math teacher, but more importantly signifies many students’ opinions that they will never use these skills outside of a classroom. In other words, students often have trouble connecting math to reality and seeing how it is applied in daily life. For instance, a student that struggles with fractions may have trouble understanding how to convert the fraction ½ to the decimal 0.50 . However, the same student has no problem understanding that “half a dollar” is equal to 50 cents. This is a great example of the disconnect students sometimes experience when struggling with math.

Studies show that math is one of the few disciplines that is accessible to all students, no matter their natural abilities. Being good at math is 1% inspiration and 99% perspiration. While natural talents and abilities will give some students an edge, math is really just about practice. That means that everyone can do well at math, despite what they might believe. Having a ‘can do’ attitude is the most important factor in math success.

As we’ve talked about in previous blog posts, learning types can be separated into three categories – visual learners, auditory learners, and tactile learners. Some students struggling with math won’t understand fractions by being told 4/8 is really “one half.” However, when visualizing a pizza with 8 slices, they suddenly understand that 4 slices would indeed be half the pizza! It is crucial for a student to recognize how mathematical concepts actually relate to real life in order for them to truly understand the material.

Do you struggle with math? Tutor Doctor can help

If you’re out there wondering why you struggle with math so much, you’re not alone. Tutor Doctor has helped thousands of students across the country achieve better grades in math with our in-home and online tutoring services . Find your nearby Tutor Doctor location today!

Reference: https://news.gallup.com/poll/16360/math-problematic-us-teens.aspx

Mathematics Clusters Reveal Strengths and Weaknesses in Adolescents’ Mathematical Competencies, Spatial Abilities, and Mathematics Attitudes

John e scofield, mary k hoard, lara nugent, joseph v lamendola, david c geary.

Author information
Article notes
Copyright and License information

Correspondence: David C. Geary, Department of Psychological Sciences, Interdisciplinary Neuroscience, University of Missouri, Columbia, MO 65211-2500, Phone: 573-882-6268, Fax: 573-882-7710, [email protected]

Issue date 2021.

Pre-algebra mathematical competencies were assessed for a large and diverse sample of sixth graders ( n = 1,926), including whole number and fractions arithmetic, conceptual understanding of equality and fractions magnitudes, and the fractions number line. The goal was to determine if there were clusters of students with similar patterns of pre-algebra strengths and weaknesses and if variation between clusters was related to mathematics attitudes, anxiety, or for a subsample ( n = 342) some combination of intelligence, working memory, or spatial abilities. Critically, strengths and weaknesses were not uniform across the three identified clusters. Lower-performing students had pronounced deficits in their understanding of mathematical equality, fractions magnitudes, and the fractions number line. Higher-performing students had particular advantages in whole number and fractions arithmetic, and the fractions number line. Students could be reliably placed into clusters based on their mathematics self-efficacy and a combination of intelligence and spatial abilities. The results contribute to our understanding of key aspects of students’ mathematical development, highlight areas in need of intervention for at-risk students, and identify cognitive areas in which scaffolds might be incorporated into these interventions.

Keywords: mathematics development, mathematics achievement, cognition, mathematics attitudes

Introduction

Students’ mathematical competencies provide a gateway to well-paying mathematics-intensive careers and contribute to ease of coping with important life decisions ( Bynner, 1997 ; Reyna et al., 2009 ). Unfortunately, there is substantial variation in the extent to which students develop these competencies, differences that persist into adulthood ( Mamedova et al., 2017 ). Most of these studies have examined the relation between early mathematical competencies and later mathematics achievement or economic outcomes based on composite achievement scores ( Duncan et al., 2007 ; Ritchie & Bates, 2013 ). These studies confirm the importance of overall mathematical competencies but do not capture the variation existing within groups of students, especially those who have difficulties learning mathematics ( Bartelet et al., 2014 ; Geary et al., 2012 ; Vanbinst et al., 2015 ). Elementary school children have relative mathematical strengths as well as weaknesses ( Geary et al., 2007 , 2012 ), but much less is known about patterns of development in middle-school students.

Performance in middle school (grades 6 to 8, 11- to 13-year-olds) mathematics is critical because it lays the foundation for success in high school (grades 9 to 12, 14- to 18-year-olds) algebra, and provides an opportunity to identify and remediate deficits beforehand. Remedial interventions are typically focused on specific competencies, such as the fractions number line or mathematical word problems (e.g., Barbieri et al., 2020 ; Fuchs et al., 2020 ), and would be most beneficial if they targeted the most pronounced deficits of at-risk students. Accordingly, one goal here was to determine if lower-achieving students showed uniform deficits in pre-algebra competencies or strengths and weaknesses in these competencies. Identifying the latter would be useful for the development of focused remedial interventions. A second goal was to determine if clusters of students with different mathematical strengths and weaknesses differed in their mathematics attitudes, anxiety, and cognitive abilities. We were particularly interested in any relation between profiles of strengths and weaknesses and spatial abilities, as a consistent relation between the latter and mathematics is found but not fully understood ( Hawes & Ansari, 2020 ; Kell et al., 2013 ; Mix, 2019 ).

The study here is part of an on-going longitudinal project that is focused on individual differences in preparation for and success in high school algebra, as related (in part) to mathematics attitudes, anxiety, and spatial abilities. A novel feature of the study is the broad assessment of pre-algebra competencies and mathematics attitudes and anxiety in a large ( n = 1,926) and diverse group of sixth graders, and the integration of measures of intelligence, working memory, and spatial abilities of a subsample of them in seventh grade ( n = 342). We used state-of-the-art clustering techniques to identify groups of sixth graders with different pattens of strengths and weaknesses in pre-algebra arithmetic and multivariate pattern analyses to identify attitudinal and cognitive differences across these clusters.

Mathematical competencies

It has been shown that success in mathematics is dependent, in part, on the adequate development of prerequisite skills ( Geary et al., 2017 ; Lee & Bull, 2016). As noted, the larger study was designed to, among other things, identify the most important prerequisite competencies needed for later success in high school algebra and the selection of prerequisite measures was based on recommendations from the National Mathematics Advisory Panel ( NMAP, 2008 ) and results of cognitive studies of mathematical development (e.g., Alibali et al., 2007 ; Braithwaite et al., 2018 , 2019 ; Siegler et al., 2011 ). Competence with whole number arithmetic was identified by the NMAP as foundational to the preparation for algebra and is predictive of concurrent ( Tolar et al., 2009 ) and longitudinal algebraic outcomes ( Casey et al., 2017 ; Siegler et al., 2012 ). We thus included a measure of fluency with whole number arithmetic.

Fractions were highlighted by the NMAP (2008) and empirical studies support their importance for preparation for algebra. For instance, elementary students’ competence with fractions predicts their later competence in high school algebra, controlling domain-general abilities and family background ( Siegler et al., 2012 ). In the United States, students typically begin to learn fractions by fourth grade (sometimes earlier). Nevertheless, about half of them struggle with correctly ordering a series of fractions in eighth grade ( Martin et al., 2007 ), and many of them do not understand that the sum of 12/13 and 7/8 is closer to 2 than 19 or 21 ( Carpenter et al., 1981 ; Hecht & Vagi, 2010 ; Mazzocco & Devlin, 2008 ). In other words, there is substantive variation in middle school students’ understanding of fractions and this variation is likely to predict variation in later algebra outcomes. Thus, we included measures of fractions arithmetic and measures that assess students’ understanding of fractions magnitudes (e.g., the fractions number line).

Eventual competence with algebra is also dependent on an understanding of several core concepts ( Booth et al., 2014 ). In an analysis of algebra errors committed by high school students, Booth and colleagues identified several persistent categories of conceptual error that predicted end of year performance. Difficulties with mathematical equality, variables (e.g., a belief they represent a single value), and mathematical properties (e.g., confusing order of operation) were the strongest predictors of later algebra performance (see also Booth & Koedinger, 2008 ). We were not able to assess all of these and focused on equivalence, as students’ difficulties here have been extensively studied ( Knuth et al., 2005 ). Middle-school students who do not understand equivalence typically interpret the ‘=‘ as a signal that the preceding numbers need to be operated on, such as added, rather than an indicator of the relation between the values to the left and right of it. Students who have an operational conception of equivalence have difficulties solving problems presented in a non-standard format, such as 6 + 3 = _ - 1, and will often indicate that the ‘=‘ means that they should solve the problem ( Alibali et al., 2007 ; McNeil et al., 2011 ; McNeil et al., 2019 ). We included non-standard format equivalence problems to assess this misconception.

Mathematics attitudes and anxiety

Eventual success in algebra and beyond can also be influenced by confidence or efficacy about one’s abilities (i.e., a personal judgement of one’s ability to perform well in future endeavors, see Talsma et al., 2018 ) and by beliefs about the later usefulness or utility of mathematics (e.g., as related to future occupation; Eccles et al., 2016 ). Several meta-analyses have revealed small but reliable relations between students’ academic efficacy and their later grades or achievement ( Talsma et al., 2018 ; Valentine et al., 2004 ), however cause-and-effect are unclear. Older students’ and adults’ academic achievement contributes to subsequent attitudes, and these contribute to later achievement. Similar bidirectional effects are sometimes ( Gunderson et al., 2018 ) but not always ( Geary et al., 2019 ) found in younger students. In any event, Lauermann et al. (2017) found reciprocal relations between mathematics self-efficacy, utility beliefs, and math-intensive career plans throughout high school, which in turn predicted employment in a mathematics-intensive profession 15 years later.

Mathematical competencies are also correlated with mathematics anxiety, although cause-and-effect relations are again not fully understood ( Carey et al., 2016 ; Devine et al., 2017 ; Hill et al., 2016 ). Mathematics anxiety is apprehension or fear associated with thoughts about engagement in mathematical activities ( Dowker et al., 2016 ). One possibility is that anxiety undermines students’ mathematical performance by the intrusion of performance-related thoughts during problem solving that in turn reduce working memory capacity and increase problem-solving errors ( Ashcraft & Kirk, 2001 ; Maloney & Beilock, 2012 ). Mathematics anxiety can also result in an avoidance of mathematics and reduced opportunities to learn ( Hembree, 1990 ; Meece et al., 1990 ). Mathematics anxiety appears to be composed of several components that could influence mathematical development and performance in different ways. The core components include anxiety about mathematics learning generally (e.g., reading a math textbook) and anxiety during mathematics evaluations ( Baloglu & Koçak, 2006 ). The former could potentially result in a general avoidance of mathematics and the latter underperformance on high-stakes tests.

If mathematics attitudes or anxiety are associated with specific clusters of pre-algebra strengths and weaknesses, they could exacerbate or ameliorate at-risk students’ engagement in middle-school mathematics and thus their preparation for algebra. To assess if there is such a relation, we included measures of mathematics utility beliefs, self-efficacy, and anxiety as related to mathematics learning and evaluations. We also included a measure of students’ attitudes about English as a contrast to their mathematics attitudes, that is, to determine if the reported attitudes were specific to mathematics.

Cognitive mechanisms

The most consistent cognitive predictors of overall mathematics achievement or longitudinal gains in achievement are intelligence and components of executive function ( Deary et al., 2007 ; Geary, 2011 ; Geary et al., 2017 ; Van de Weijer-Bergsma et al., 2015 ). The latter includes updating or holding something in mind (often called working memory), inhibition of task-irrelevant information, and shifting from one task to another and then appropriately returning to the first ( Miyake et al., 2000 ). Of these, the most consistent predictor of mathematics achievement is updating or working memory ( Bull & Lee, 2014 ; Friso-van den Bos et al., 2013 ). These cognitive abilities are particularly important for mathematics learning because of the highly abstract nature of the material and the continual introduction of new material during schooling. Although the focus of the larger project is on spatial abilities, we included measures of working memory and intelligence as controls.

One goal, as noted, of the larger project is to examine the relation between spatial abilities and ease of learning spatial-related aspects of algebra (e.g., recognizing how common functions map to coordinate space) in high school. On the basis of this goal and a consistent finding of a relation between spatial and mathematical abilities ( Geer et al., 2019 ; Hawes & Ansari, 2020 ; Mix, 2019 ; Mix et al., 2016, 2017 ), we included three measures of spatial competence – visuospatial working memory, visuospatial attention, and mental rotation – in the study. We included three measures because the relative importance of different components of spatial ability could vary with the complexity and content of the mathematics assessments ( Bull et al, 2008 ; Geary et al., 2007 ). For instance, Gilligan et al. (2020) found that a short-term intervention that enhanced skill at rotating objects improved performance on missing item problems (e.g., 2 + = 7), whereas enhancement of sensitivity to proportional relations improved accuracy in placing numerals on the number line.

Visuospatial short-term memory appears to be involved in an array of mathematical domains, especially in later grades, but these specific relations are not fully understood ( De Smedt et al., 2009 ; Li & Geary, 2017 ; Swanson et al., 2008 ). Visuospatial attention contributes to the ability to represent and compare the relative magnitude of numerals ( Longo & Lourenco, 2007 ; Zorzi et al., 2012 ) and is more strongly related to performance on the fractions number line than are other spatial abilities, such as visuospatial working memory ( Geary et al., 2020 ). The latter finding appears to be consistent with the results of Gilligan et al. (2020) ; specifically, focusing students’ attention on proportional distance improved number line performance. More complex spatial abilities (including mental rotation) are related to some aspects of mathematical abilities ( Mix & Cheng, 2012 ), and may become increasingly important as mathematical development shifts from number/arithmetic to algebra/geometry ( Casey et al., 1995 ; Kyttälä & Lehto, 2008 ).

Current study

The current study extends prior work with the inclusion of multiple mathematical competencies in a single assessment and in doing so enabled an examination of patterns of strengths and weaknesses in a large and diverse sample of lower- and higher-achieving students. The study also contributes to prior work by simultaneously identifying the attitudinal, anxiety, and cognitive strengths and weaknesses that emerge in different achievement clusters. More precisely, we used state-of-the-art clustering procedures to identify groups of students with different patterns of pre-algebra mathematical strengths and weaknesses and multivariate pattern analysis to identify attitudinal and cognitive predictors of cluster membership.

An assessment of whether intelligence, working memory, or one or several forms of spatial ability are associated with weaknesses in pre-algebra competencies could have implications for the development of remedial interventions. This is because interventions that include scaffolds that accommodate cognitive weaknesses are more successful in remediating at-risk students’ mathematical deficits than are interventions that do not include them (e.g., Fuchs et al., 2020 ). Information on the cognitive correlates of students with an at-risk profile of pre-algebra competencies would identify both areas of potential intervention and provide insights into the type of scaffold that might enhance remediation efforts. Similarly, the identification of attitudes or anxiety that predict cluster membership could indicate additional areas of remediation.

Participants

The original sample included 2,027 sixth graders who were assessed across two cohorts ( n s = 1,157, 870) conducted in collaboration with the Columbia Public Schools in Columbia, MO. Data were missing for 101 of these students (e.g., no information on student sex), leaving 1,926 of them for the analyses of mathematics performance and attitudes. The first cohort included approximately 86% of all sixth-grade students enrolled the district. The remaining 14% of students were absent the day of the assessment or unable to participate. The second cohort included 83% of invited sixth graders. The sampling for the two cohorts occurred in consecutive academic years and were otherwise identical, with the exception that one school was omitted for the second cohort because of over-representation of students from this school (from the first cohort) in the longitudinal sample. As part of an on-going longitudinal study, 342 students from the sixth-grade sample were tested again in seventh grade

Demographic information was not available for the sixth-grade sample but should be very similar to that of the district as a whole. For the district, sixth-graders were 61% white, 20% black, 5% Asian, 7% Hispanic, and 6% multiracial, and 43% qualified for free or reduced lunch. Demographic information was obtained through a parent survey ( n = 281) for the longitudinal sample. Eighty-eight percent of the students were non-Hispanic, 6% Hispanic or Latino, with the remaining unknown. The racial composition of the sample was 70% White, 14% Black, 3% Asian, 1% Native American, 10% multi-racial, and the remaining unknown. Self-reported annual household income was as follows: $0-$24,999 (12%); $25,000-$49,999 (18%); $50,000-$74,999 (12%); $75,000-$99,999 (22%); $100,000-$149,999 (19%); and $150,000+ (17%). Seventy-one percent of the students had at least one parent with a college degree. Sixteen percent of families received food assistance, and six percent housing assistance.

Mathematics Tests

The tests, detailed instructions, and raw data for the key analyses are available on OSF. The assessment included an Exponents and Radical Rules Test that is not reported here because of a high nonresponse rate, and an Equal Sign task due to a low number of trials. All tests were administered using paper-and-pencil for the first cohort, and the Equality Problems, Fractions Comparison Test, Fractions Number Line, and Academic Attitudes and Mathematics Anxiety were assessed using iPads for the second cohort. There were only 2 significant cohort effects (all other p’ s > .07), whereby students in the first cohort scored higher on the arithmetic fluency ( p = .002, d = .14) and fractions comparison test ( p = .0003, d = .17). Given the null effects for all other measures and the small difference for the arithmetic fluency and fractions comparison test, the two cohorts were combined.

Arithmetic fluency.

The test included 24 whole-number addition (e.g., 87 + 5), 24 subtraction (e.g., 35 – 8), and 24 multiplication (e.g., 48 × 2) problems. Students had 2 min to solve as many problems as possible. A composite arithmetic fluency score was based on the number correct across the three operations ( M = 18.94, SD = 6.25; α = .57). Despite the relatively low reliability, performance on this measure is more strongly correlated with mathematics ( r = .62) than reading achievement ( r = .32), indicating the measure shows both convergent and discriminant validity.

Equality problems.

Students who struggle with mathematical equality have difficulties with problems in non-standard formats, such as 8 = __ + 2 – 3. Thus, we created a 10-item test in multiple choice format (4 options) to assess competence at solving such problems. 3.7% of the items were unanswered and scored as incorrect. A composite was the mean percent correct for the 10 items ( M = 79.99, SD = 23.89, α = .80).

Fractions arithmetic.

The items were sets of twelve addition (e.g., 1/3 + 1/6), twelve multiplication (e.g., 1/4 × 1/8), and 10 division (e.g., 2 ÷ 1/4) problems. Students had 1 min for each operation. The score was the number of correctly solved problems ( M = 10.33, SD = 6.91; α = .62). Despite the relatively low reliability, performance on this measure is more strongly correlated with mathematics ( r = .70) than reading achievement ( r = .41), indicating the measure shows both convergent and discriminant validity.

Fractions comparison.

For each of 48 pairs, students circled the larger of two fractions, within 90 sec. There were four item types that reflect common problem-solving errors and strategies (see Geary et al., 2013 ). In the first type the numerator is constant, but the denominator differs (e.g., 2/4 2/5), which assesses students’ understanding of the inverse relation between the value of the denominator and the quantity represented by the fraction. In the second type numerators have a ratio of 1.5 and denominators a ratio between 1.1 and 1.25 (e.g., 3/10 2/12), making identification of the larger magnitude easier using numerators (correct) than denominators (incorrect). Numerators and denominators in the third type are reversed (e.g., 5/6 6/5), which requires students to choose the fraction with the larger numerator and smaller denominator. The final type involves skill at using 1/2 as an anchor for estimating fraction values (e.g., 20/40 8/9). The foils are always close to one but contain smaller numerals than the 1/2 fraction. A composite was based on performance (correct – incorrect; M = 16.70, SD = 15.32) across the four item types ( α = .87).

Fractions number line.

Students sequentially placed 10 fractions (10/3, 1/19, 7/5, 9/2, 13/9, 4/7, 8/3, 7/2, 17/4, 11/4) that were centrally presented in large font onto the 0-to-5 number line ( Siegler et al., 2011 ), and 94.4% of the lines were completed within a 4 min time limit. The data for the remaining 5.6% of lines were estimated using a multiple imputations procedure in SAS (2014) . Individual items were scored as the absolute percent deviation between the placement and the correct location, which were averaged across the 10 items ( M = 20.50, SD = 14.09, α = .85), and then multiplied by −1 so that higher scores represent more accurate placements.

Academic attitudes and anxiety

The grade-appropriate mathematics and English language attitudes measures were from the Michigan Study of Adolescent and Adult Transitions ( http://garp.education.uci.edu/msalt.html ) and are designed to assess students’ self-evaluated efficacy and their beliefs about the long-term utility of competence in these areas ( Eccles & Wigfield, 2002 ; Meece et al., 1990 ). The mathematics attitudes measure included seven items on a 1-to-7 Likert scale; e.g., “How much do you like doing math?” rated from 1 (“a little”) to 7 (“a lot”), with six similar English items. We used three approaches to determine their factor structure, including an exploratory principle component analysis (PCA) with promax rotation ( SAS, 2014 ), as well as parallel and MAP analyses ( R Core Team, 2017 ).

Mathematics and English attitudes.

The MAP analysis suggested one component, but the eigenvalues from the PCA and the parallel analysis suggested two factors. The factor loadings were consistent with distinct utility (Items 1 to 4, inclusive) and self-efficacy (Items 5 to 7, inclusive) dimensions. The scores were the mean of the corresponding items (α = .77 for utility; 84 for self-efficacy). All of the procedures indicated a single factor for English Attitudes, which was scored as the mean of the six items (α = .85).

Mathematics anxiety.

The 10 items were adapted from Hopko, Mahadevan, Bare, and Hunt (2003) . Each item (e.g., “Taking an examination in a math course”) was rated on a 1 (induces low anxiety) to 5 (induces high anxiety) scale. All three analyses indicated two factors. The first was defined by five items that involved learning mathematics (e.g., “Having to use the tables in the back of a math book”). The second factor was defined by four items that involved some type of evaluation (e.g., “Taking an examination in a math course”), and one other item (i.e., “In general, how anxious are you about math?”). Composite scores were based on the mean of the five learning anxiety items (α = .78) and the five evaluation anxiety items (α = .84).

Standardized Measures

Intelligence..

Students in the longitudinal component were administered the Vocabulary and Matrix Reasoning subtests of the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999 ). Based on standard procedures, subscale scores were used to generate an estimated full-scale IQ. The intelligence of the longitudinal sample was average ( M = 105, SD = 13).

Achievement.

For the longitudinal cohort, mathematics and reading achievement was assessed with the age-appropriate Numerical Operations (NO) and Word Reading (WR) subtests from the Wechsler Individual Achievement Test–Third Edition ( Wechsler, 2009 ), respectively. The NO included basic arithmetic and continued through fractions, algebra, geometry and calculus. The WR assessed single word reading, beginning with 1-syllable words and progressing to more complex vowel, consonant, and morphology types. The mathematics ( M = 100, SD = 19) and reading ( M = 104, SD = 13) achievement of the students in the longitudinal sample was average.

Cognitive measures

The cognitive tasks were administered using iPads using customized programs developed through Inquisit by Millisecond ( https://www.millisecond.com ) or through Qualtrics ( https://www.qualtrics.com ). Manuals and detailed descriptions of these tasks are available at Open Science Framework ( https://osf.io/qwfk6/ ) and are all standard measures of working- and short-term memory, and spatial ability. A verbal memory task was assessed (described in the SOM ) but not reported here as we focused a-priori of working memory and spatial abilities.

Digit span.

Forward and backward digit span measures were administered, following Woods et al. (2011) . Digits were auditorily (using the iPad) and sequentially presented at 1s intervals, beginning with 3 digits for the forward task and 2 digits for the backward task. Students were asked to tap the digits on a circular display after the sequence in forward/backward order. Correct responses increased the sequence length for the following trial, and two consecutive errors reduced the sequence length. Each task terminated after 14 trials. The longest digit sequence correctly recalled before two consecutive errors at the same length was scored as the span ( M = 5.71, 4.59, SD = 1.12, 1.20 for the forward and backward, respectively).

Following Jaeggi et al. (2010) , a similar version of a single n-back task with letters was administered. A “target” letter and then a sequence of 20 stimulus letters was presented (all consonants; 6 are target; 14 are not; randomly determined), Students indicated whether the currently presented letter is a target by tapping a key within a 3,000 ms response period (500ms + 2,500ms blank ITI), otherwise withholding a response. Target letters were either the very first stimuli of the sequence (N = 0), the same as the one immediately preceding it (N=1), or as the one in the two (N = 2) or three (N=3) preceding trials. After several practice items, students began on level N = 0. Across five blocks, students either moved up, down, or remained at a level (<3 errors – move up; 3–5 errors – repeat level; >5 errors – move down). Feedback (% correct) was displayed after each block. The score ( M = 3.80, SD = 0.76) was calculated as (Hits – False Alarms) / (total blocks).

Spatial span.

The Corsi Block Tapping Task was administered ( Kessels, van Zandvoort, Postma, Kappelle, & de Haan, 2000 ). Students viewed a display of nine squares (appearing randomly arranged) that “lit up” in a predetermined sequence and tapped on the squares in the same order they were lit. Sequences started at two squares and increased up to nine squares. Students had two attempts at each sequence length. Correct responses were followed by an increase in sequence length, and two incorrect responses at a given level terminated the task. The score is the total number of correctly recalled sequences across the entire task ( M = 8.34, SD = 1.83).

Spatial ability.

The first spatial measure was the Judgment of Line Angle and Position Test (JLAP; Collaer, Reimers, & Manning, 2007 ). Here, students matched the angle of a single presented line to one of 15-line options in an array at the bottom of the screen. There were 20 test items sequentially presented. Stimuli were presented for a maximum of 10s, with the trial terminating when the student made a selection. The JLAP was scored as the number correct ( M = 13.33, SD = 3.03).

The second measure used was the Mental Rotation Task (MRT-A; Peters et al., 1995 ). On each of 24 trials, students viewed 3D images of 10 connected cubes. On each trial, there was one target and four response options, requiring students to select the two options that were the same figure, only rotated to various degrees. After four practice problems, students completed two blocks of 12 problems each with a 3 min per block time limit. The MRT was scored as the number of problems on which both correct responses were chosen ( M = 8.75, SD = 4.13).

During a 45 min assessment, groups of 14 to 32 students were administered the mathematics tests and academic attitudes measures in their classroom (Age : M = 146.88 months , SD = 4.51). For the longitudinal component, tasks were individually administered in 45 min sessions in a quiet location in their school. The cognitive measures were administered in the fall semester (Age: M = 152.63 months, SD = 4.45) and the achievement and attitudes measures in the spring (Age: M = 156.79 months, SD = 4.41). Tasks were administered in a fixed order across participants. Parents provided informed written consent, and assent was obtained from adolescents for all assessments. The University of Missouri Institutional Review Board (IRB; Approval # 2002634, “Algebraic Learning and Cognition”) approved all methods included in this study.

Individual continuous mathematics measures were standardized ( M = 0, SD = 1), and the attitudes and anxiety measures were standardized to M = 100 ( SD = 15). Hierarchical cluster analyses (Ward’s method) were used to identify subsets of students with different math competence profiles. The stability of the cluster solution was validated using the Bootstrapped Jaccard similarity coefficient (shortened to J ; see Hennig, 2007 for details), with values above 0.6 interpreted as acceptable. Between-subjects ANOVAs (and Bayes Factor ANOVA equivalents) were used to test differences across clusters. A “leave-one-out” (LOO) cross-validation approach was also used for testing cluster differences in each mathematics measure. For example, to test cluster differences between performance on the fractions number line, the cluster analysis was re-estimated using every measure except for the fractions number line. This ensures that cluster differences on a given test reflects a novel, out-of-sample test, thus avoiding issues of circularity.

For the sixth-grade attitudes and anxiety measures and cognitive measures from the longitudinal component, multivariate pattern analyses (MVPA; logistic regression classifier, L2 penalty, C = 0.5) using the scikit-learn module in python was used to predict students’ identified math cluster. A similar LOO cross-validation was used for model training and testing to ensure each students’ prediction was a novel out-of-sample case left out of model training. Classifier accuracy is reported here, with chance being 33.3% (three possible cluster labels). Model significance was tested through permutation testing, which entails randomly shuffling the cluster labels of students and re-training the classifier 500 times on the shuffled data. Significance is reported as the proportion of times the shuffled data accuracies exceeded the true observed accuracy.

To further elucidate the relative contributions of each specific predictor, a Bayesian model comparison approach was used ( Rouder, Engelhardt, McCabe, & Morey, 2016 ). Cluster labels were used as the dependent measure, with the six cognitive measures and IQ, or the five attitude/anxiety measures, as predictors. To assess evidence for the inclusion/exclusion of a certain predictor (e.g., digit span), ratios of Bayes Factors (BFs) were taken from the best model that included a certain predictor (e.g., digit span, MRT, and JLAP) to the model that excluded it (only MRT and JLAP). All analyses were performed using R (v.3.5.1) and python (v.3.7.4). Main statistical interpretations are based on Bayesian statistics ( Bayes Factor package using default priors), where BFs < 1 indicate evidence for the null hypothesis, 1–3 weak/ambiguous evidence, and > 3 as evidence for the alternative hypothesis ( Kass & Raftery, 1995 ). As a supplement, frequentist statistics are also presented alongside each analysis, as using multiple estimates can often be informative in model evaluation ( Valentine, Buchanan, Scofield, & Beauchamp, 2019 ).

Correlations among the sixth-grade mathematics variables and the cognitive, attitudes, and achievement measures are shown in Table 1 ; correlations among the seventh-grade cognitive and achievement measures are in the SOM and data used in the analyses are available in OSF ( https://osf.io/wqjv7/ ).

Correlations between the mathematics variables and cognitive and attitudes variables.

Note. correlations > |.11| are significant, p < .05.

Table 2 presents descriptive statistics for the sixth-grade and longitudinal sample variables; code for the full statistical analyses are available in the SOM. The clustering analysis was applied to the standardized scores for individual mathematics measures. Two main clusters were first identified, segregating students into high ( n = 1,429; J = .758) and low ( n = 497; J = .608) groups. Figure 1A shows a radar chart for the two main clusters (high and low), where values closer to the center indicate lower performance and values closer to the perimeter of the circle indicate higher performance. For all five mathematics measures, clear high-low differences emerged ( BF 10 ’s ≥ 1.3e +98 , p ’s < .001), and were maintained when using the left-out validation test measures ( BF 10 ’s ≥ 2.2e +65 , p ’s < .001). More interestingly, from inspection of the cluster solution (visual inspection of the cluster dendrogram; see supplemental materials ) and examining cluster stability, it was apparent that the high group was further divided into two higher subgroups, creating a total of three groups overall. For the remainder of the analyses, we discuss these as low ( n = 497; J = .683), medium ( n = 1,001; J = .649), and high ( n = 428; J = .692) groups.

Descriptive statistics for the low, medium, and high groups

Note. The individual mathematics variables are centered ( M = 0, SD = 1), and the intelligence and numerical operations are standardized ( M = 100, SD = 15). Effect sizes (Cohen’s d ) are presented in two ways. First, to highlight deficits in the lowest groups, Cohen’s d is calculated comparing the low group versus the medium and high group together (one vs. rest approach). Likewise, the high group advantages highlight the relative differences between the high group and both the low and medium groups.

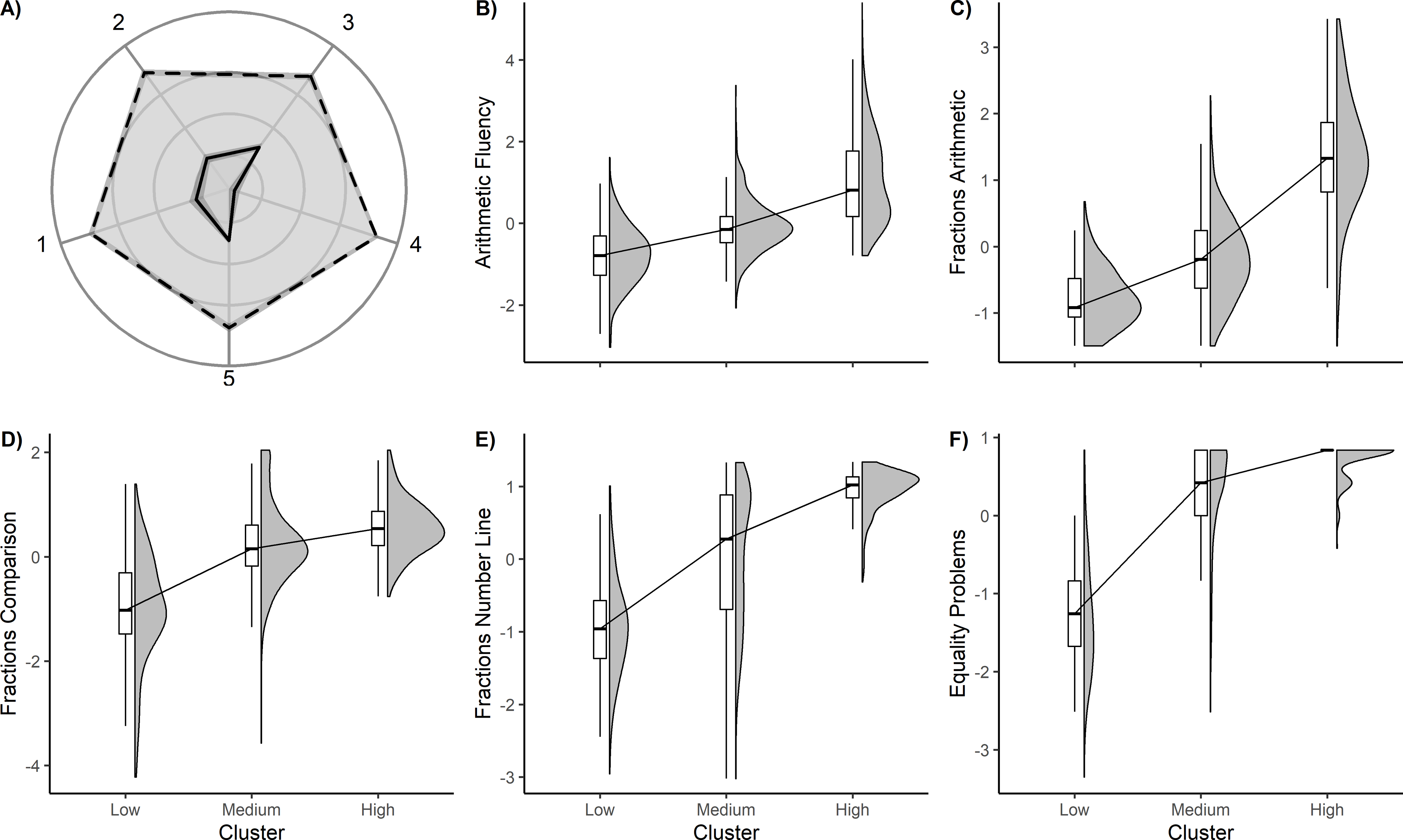
A) Radar chart of sixth grade mathematics measures from the two (high, low) cluster solution; lower scores are near the center and higher near the periphery. Clear high (dashed) and low (solid) groups are evident across all measures. 1 = Fractions comparison; 2 = Fractions number line; 3 = Arithmetic fluency; 4 = Equality problems; 5 = Fractions arithmetic. B-F) Boxplots depicting the median and first and third quartiles across the three clusters for each mathematics measure. To the left of each boxplot is a density plot showing the distribution of scores.

When analyzing differences among the three clusters, we observed strong main effects across all five measures; Arithmetic fluency, BF 10 = 6.8e +218 , F (2,1923) = 676.35, p < .001; Equality problems, BF 10 = 3.3e +428 , F (2,1923) = 1746.59, p < .001; Fractions arithmetic, BF 10 = 7.8e +376 , F (2,1923) = 1431.61, p < .001; Fractions comparison, BF 10 = 3.1e +180 , F (2,1923) = 532.09, p < .001; and, Fractions number line, BF 10 = 9.7e +234 , F (2,1923) = 741.08, p < .001. Post-hoc independent-samples t -tests (Tukey’s HSD) revealed significant differences across all clusters and measures ( p ’s < .001; Low < Medium < High). While students composing the clusters showed the same graded pattern among measures, their strengths and weaknesses were not uniform. As shown in Table 1 , the low group (as compared to the medium and high groups combined) had especially pronounced deficits for the equality problems, fractions comparison, and the fractions number line. Higher performing students (as compared to the medium and low groups combined) had especially high performance in fractions arithmetic, arithmetic fluency, and the fractions number line. Figure 1B – 1F shows mean differences across clusters for the mathematics measures. Importantly, we validated these patterns of strengths and weaknesses and overall cluster differences using a LOO cross-validation approach, and main effects for all measures remained strong ( BF 10 ’s ≥ 2.9e +66 , p ’s < .001).

Attitudes and mathematics anxiety

Next, we tested how self-reported attitudes and anxiety measures related to the clear differences found in the objective mathematics measures. We found strong evidence for a main effect of cluster for mathematics utility, BF 10 = 2.0e +7 , F (2,1922) = 22.54, p < .001, and an even larger effect for mathematics efficacy, BF 10 = 2.8e +50 , F (2,1922) = 130.91, p < .001. In a graded fashion, attitudes about mathematics utility and efficacy increased across cluster groups ( p ’s ≤ .001; Low > Medium > High; Figure 2A – 2C ). This was not the case, however, with attitudes about English. While still significant using frequentist statistics [ F (2,1922) = 5.87, p = .003], Bayesian evidence revealed a severely dampened effect of English attitudes ( BF 10 = 2.1) compared to the strong effects found in mathematics attitudes. Both mathematics anxiety measures showed significant cluster effects: Evaluation, BF 10 = 5.0e +7 , F (2,1922) = 23.47, p < .001; Learning, BF 10 = 2.0e +35 , F (2,1922) = 91.68, p < .001. Post-hoc comparisons showed that in both measures, there were decreases in anxiety from the low- to high-cluster groups ( p ’s ≤ .004; High < Medium < Low), which are visualized in Figure 2D – 2E .

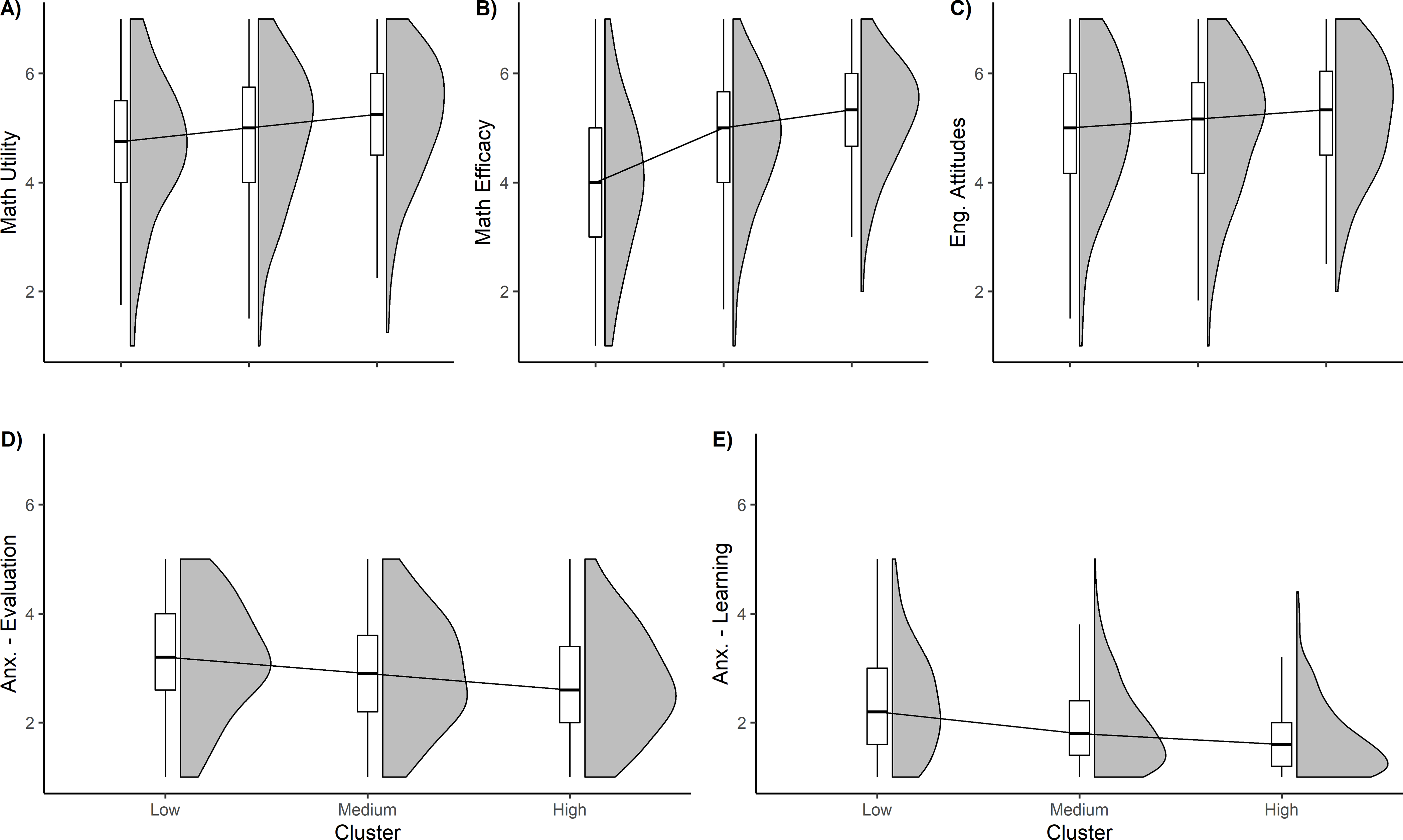
Boxplots illustrating the median and first and third quartiles across the three clusters for A-C) mathematics and English attitudes, and D-E) mathematics anxiety. To the left of each boxplot is a density plot showing the distribution of scores.

As an alternative to the mass univariate analyses presented above, MVPA classifiers were used to predict students’ cluster labels from the multivariate relationships of the five attitudes and anxiety measures. This is an especially useful approach when analyzing factors that are external to the clustering analysis. Using a LOO cross-validated logistic regression classifier, a model using these five measures was able to predict cluster membership with 55.0% accuracy (see Figure 3 ). Permutation testing confirmed this to be above chance accuracy, p < .001 (with chance performance at 33.3%). Bayesian model comparisons clearly identified mathematics efficacy as the measure contributing the most to cluster differences (see Table 3 ). BF 10 ’s for mathematics utility, anxiety for evaluation, anxiety for learning, and English attitudes were all < 1 (evidence for the null hypothesis) compared to models including mathematics efficacy. Indeed, the best overall model was for efficacy alone, BF 10 = 445.44 against an intercept only model. Comparing the model including all five predictors to one excluding efficacy showed the importance of efficacy ( BF 10 = 30.52) while controlling for all other predictors.

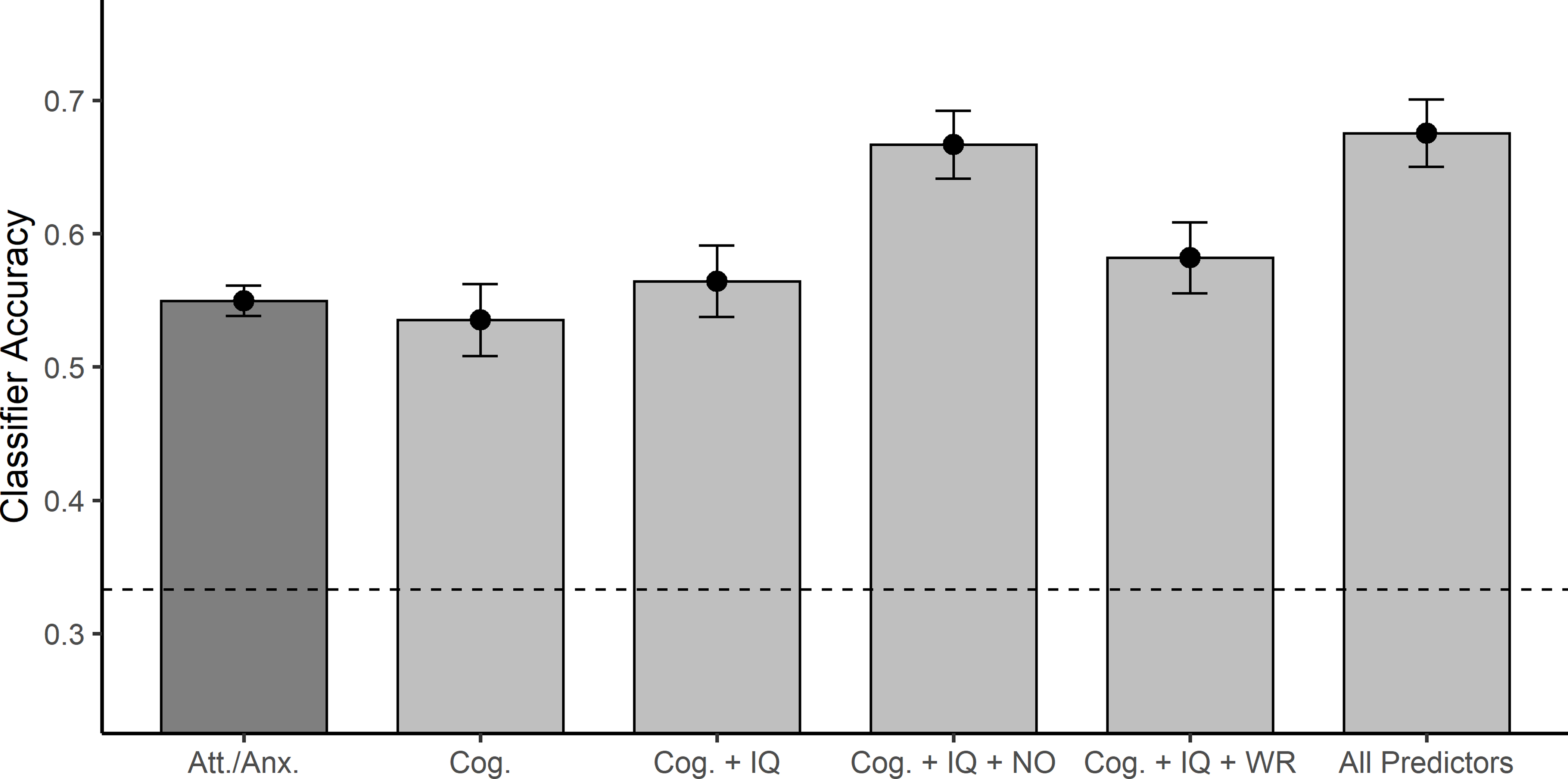
Accuracy of classifying students into their respective clusters (with standard error of the mean) using the variables noted on the x -axis (see text). The darker gray for the attitudes and anxiety indicates this model was trained using the sixth-grade sample. All other models were trained using the longitudinal data. All predictors indicates that the model was trained using the six cognitive measures, IQ, Numerical Operations, Word Reading, and the attitudes and anxiety measures. Cog. = the working memory and spatial measures; NO = Numerical Operations; WR = Word Reading; Att./Anx. = mathematics attitudes, anxiety, and English attitudes. The dashed horizontal bar indicates chance performance at 33.33%. All models were significantly above chance performance from permutation testing.

Bayes Factors for individual and combined predictors

Note . Bayes Factors for a given predictor, controlling for the contributions of each other predictor in the model

Cognitive Measures

The last set of analyses sought to test the prediction that students’ cognitive performance in seventh grade was related to and can predict mathematics competence from the end of the previous year. Univariate analyses showed strong main effects of cluster across all cognitive variables: Digit span forward, BF 10 = 2.4e +6 , F (2,339) = 20.56, p < .001; Digit span backward, BF 10 = 8.7e +8 , F (2,339) = 27.69, p < .001; N-back, BF 10 = 8.3e +8 , F (2,339) = 27.61, p < .001; Spatial span, BF 10 = 1.2e +7 , F (2,339) = 22.45, p < .001; Judgment of Line Angle and Position, BF 10 = 1.1e +6 , F (2,339) = 19.58, p < .001; Mental Rotations Test, BF 10 = 2.3e +6 , F (2,339) = 20.55, p < .001. Intelligence was additionally assessed in the longitudinal component, BF 10 = 4.1e +24 , F (2,339) = 75.98, p < .001. With intelligence showing strong effects across the different clusters, we re-assessed the cognitive differences while controlling for intelligence, and all predictors retained their effects ( BF 10 ’s ranging from 13.15 to 347, p ’s ≤ .05) with the exception of the Mental Rotations Test ( BF 10 = 0.421, p = .089). As seen in Figure 4A - 4I , graded effects of cognitive differences are evident, similar to the attitudes and anxiety measures, (all p ’s ≤ .007; Low < Medium < High).

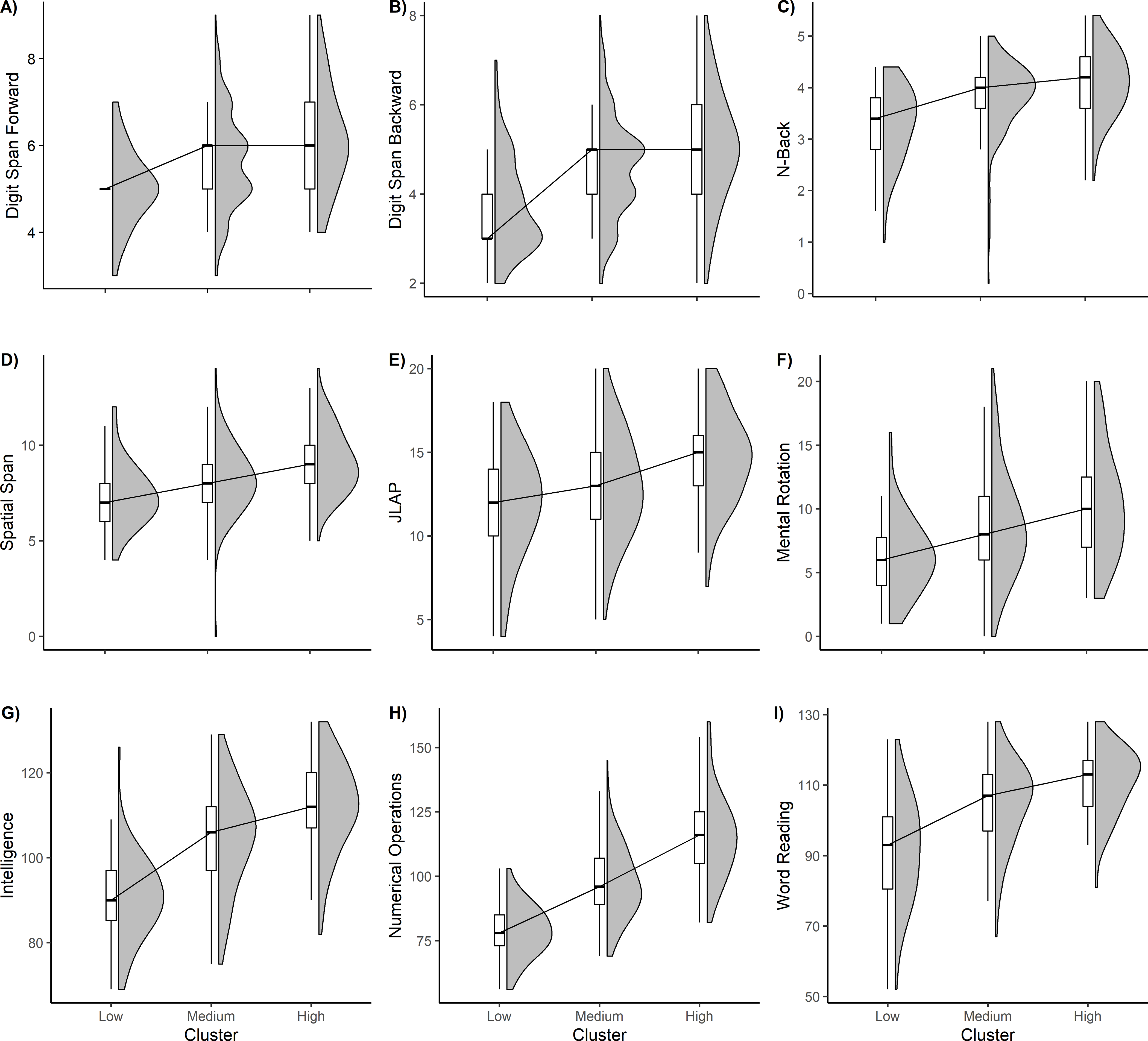
Boxplots illustrating the median and first and third quartiles across the three clusters for A-F) the six cognitive measures, and G-I) intelligence, Numerical Operations, and Word Reading. To the left of each boxplot is a density plot showing the distribution of scores.

Next, a similar logistic regression classifier was trained and validated to predict cluster membership, this time solely using the six cognitive measures. We were able to predict cluster membership with a classification accuracy of 53.51%, which was significantly above chance, p < .001. As strong IQ differences were seen across clusters, IQ scores were added to the cognitive measures, which improved classification accuracy to 56.4%. While post-hoc comparisons may have indicated larger deficits and strengths in measures of working memory before controlling for IQ, Bayesian model comparisons ( Table 2 ) showed that individually, both spatial span and performance on the JLAP contributed the most to cluster differences ( BF 10 ’s of 3.62 and 4.06, respectively). However, the overall best model was one that included JLAP, spatial span, as well as IQ. Thus, a combination of measures resulted in above chance accuracies, above the contribution of any single predictor. Spatial span with JLAP ( BF 10 = 54.45) appeared to contribute more than either spatial span with IQ ( BF 10 = 24.10), or JLAP with IQ (39.23).

For completeness, Numerical Operations and Word Reading scores in seventh grade were also considered. Numerical operations showed large across-cluster differences in the expected direction (Low < Medium < High), BF 10 = 9.1e +42 , F (2,339) = 146.48, p < .001, as did Word Reading scores, BF 10 = 5.7e +18 , F (2,339) = 56.82, p < .001. Indeed, adding Numerical Operations scores to the cognitive predictors and IQ increased cluster classification accuracy to 66.7%, p < .001, and to a lesser extent with the addition of Word Reading scores, 58.2%, p < .001 (see Figure 3 ). Notably, adding the sixth-grade attitudes/anxiety variables to the model including the cognitive measures, IQ, Numerical Operations, and Word Reading minimally improved classification accuracy (67.5%, p < .001) compared to the alternative models. However, these results show that later cognitive performance of students can reliably predict across-grade mathematical competencies, underscoring the importance of mathematical differences in its relation across different domains.

The primary contributions of the current study include a broad assessment of pre-algebra competencies and the identification of clusters of students with similar patterns of strengths and weaknesses in these competencies, as well as identifying the attitudes and cognitive abilities that best discriminate the clusters. Moreover, we applied state-of-the-art clustering techniques and multivariate pattern analyses to the performance of students in a larger and more diverse sample than is typical in these types of studies. As the reader knows, the use of these methods resulted in the identification of three clusters of students with different patterns of pre-algebra strengths and weaknesses. The results make theoretical and practical contributions to our understanding of mathematical development, but the focus here is on the lowest performing students This is because their patterns of strengths and weaknesses provide useful information on where to best focus intervention efforts. The cognitive abilities that best classify students into groups provide potentially useful information on the types of scaffolds that might be included in any such interventions.

Mathematics competencies

The lower-performing students had deficits across mathematical areas, but critically these were not uniform, in keeping with studies of younger students who have difficulties with mathematics learning ( Geary et al., 2012 ). In support of recent work by Siegler and colleagues ( Braithwaite et al., 2019 ; Siegler et al., 2011 ) and McNeil and colleagues (e.g., McNeil et al., 2019 ), the lower-performing students had particularly large deficits in their understanding of fractions magnitudes and mathematical equality. If early deficits in these areas predict later performance in algebra – a planned assessment for the current project once data collection is completed – controlling other factors (e.g., intelligence, parental education), then they could be used as a quick screening measure to identify at-risk students before they enter middle school. This would not mean that these are their only deficits but would indicate a broader assessment of their strengths and weaknesses is warranted. Whatever their performance in other areas, targeted interventions in these domains would be an important component of better preparing them for success in algebra. This is because an understanding of fractions and mathematical equality have been found to predict later performance in algebra ( Booth et al., 2014 ; Booth & Koedinger, 2008 ; Siegler et al., 2012 ).

The fraction deficits of these lower-performing students were evident with the simple comparison of the magnitudes of two fractions and in terms of their skill at situating fractions magnitudes on the number line. A strikingly ( d = 2.95) poor understanding of mathematic equivalence also stood out among the lower-performing students. The magnitude of these students’ deficits here was roughly double their relative deficits on the fraction measures and more than double their relative cognitive deficits. We did not have information on how they were approaching these problems, but the results are in keeping with a rigid operational view of the ‘=‘ ( Alibali et al., 2007 ; McNeil et al., 2011 ; McNeil et al., 2019 ). Whatever they were doing, the results here add substantial weight to the argument that mathematical equivalence is a key part of students’ conceptual understanding of mathematics and that a poor understanding of this concept slows mathematical development.

The higher-achieving students had particularly large advantages in computational fluency with whole number and fractions arithmetic, that is, larger advantages than might be expected based on their cognitive performance and intelligence. Fluency is dependent on the memorization of basic facts and procedures and for fractions arithmetic is dependent on a conceptual understanding of these procedures (e.g., that multiplying proper fractions results in smaller magnitudes; Braithwaite et al., 2019 ; Braithwaite et al., 2018 ). A relatively better understanding of fractions is also indicated by their strong performance on the fractions number line that in turn may have been facilitated by their ability to transform fractions (e.g., 17/4 = 4 1/4; Siegler et al. 2011 ). These advantages in number development and computational fluency are very likely to result in later advantages in learning algebra above and beyond the contributions of cognitive abilities (NMAP, 2008; Siegler et al., 2012 ). Moreover, these results suggest that achieving computational fluency is an important part of mathematical development, likely because fluency will reduce the working memory demands associated with solving more complex problems in which basic facts and procedures are embedded ( Geary & Widaman, 1992 ; Sweller, van Merriënboer, & Paas, 2019 ).

The important point is that the results from our large and diverse sample are consistent with previous studies and confirm that a poor understanding of fractions magnitudes and mathematical equivalence are core deficits of low-achieving students. A unique contribution here is that these deficits are evident above and beyond their more general mathematics deficits. The pattern of results shown here is useful not only in identifying and targeting specific deficits, but in identifying areas in which higher-performing students especially excel. The latter was most evident on the measures of fluency of solving whole number and fractions problems, which was highlighted by the NMAP (2008) as foundational to preparation to algebra. The implication is that any interventions that focus on at-risk students’ conceptual understanding of fractions and mathematical equivalence should not do so at the expense of building procedural fluency. The relative importance of these different pre-algebra skills in predicting later algebra outcomes is not currently known but will be assessed in the on-going longitudinal component of the study.

Students’ performance in mathematics, whether it was toward the low- or high-end, had little relation to their attitudes about English. The result indicates that students were differentiating between English and mathematics and that difficulties with mathematics might not be associated with negative attitudes about schooling more broadly, at least for sixth graders. In keeping with many previous studies, the lower-performing students had a lower mathematics self-efficacy, lower beliefs in the utility of mathematics, and higher levels of mathematics anxiety for both learning and evaluation than did their higher-performing peers ( Ashcraft & Kirk, 2001 ; Carey et al., 2016 ; Dowker et al., 2016 ; Hill et al., 2016 ; Maloney & Beilock, 2012 ). However, when controlling for these various attitudes and anxiety measures instead of analyzing them individually, mathematics self-efficacy stood out in terms of predicting cluster membership. A striking result of this is the weaker relation between mathematical competencies and all other attitudes and anxiety once controlling for self-efficacy, in support of results found by Devine et al. (2017) , that is, that many students struggling with mathematics do not show particularly high levels of mathematics anxiety.

The disconnect between the lower-performing students’ attitudes and their actual competencies is illustrated by a contrast of the differences between them and their typically-achieving (middle cluster) peers. Differences in mathematics ranged from d = 1.19 to 2.95 ( M = 1.7), but group differences for mathematics self-efficacy, the best predictor of cluster membership, showed a Cohen’s d of 0.75 ( Cohen, 1988 ). The latter is less than half the size of their actual mathematics deficits, with even starker disconnects for the anxiety measures. These patterns are consistent with the broader Kruger-Dunning effect, whereby lower-performing individuals significantly over-estimate their relative competencies in many domains ( Kruger & Dunning, 1999 ). The reasons for the disconnect between actual performance and estimates of relative performance are widely debated and include statistical regression, poor meta-cognition, and insensitivity to the commission of errors, among others ( Gignac & Zajenkowski, 2020 ; Jansen, Rafferty, & Griffiths, 2021 ; McIntosh, Fowler, Lyu, & Della Sala, 2019 ). The Kruger-Dunning effect is not generally integrated within studies of children’s academic development, but our results suggest that such an integration might be fruitful.

It is not clear what is underlying the effect in this sample, but one potential contributing factor is that these students are receiving inaccurate feedback about their mathematical development and thus might not fully appreciate the difficulties they will face in high school algebra. At the same time, whatever is maintaining their self-efficacy and keeping their anxiety in check could serve as a protective mechanism as they move forward in their mathematics education.

Cognitive performance

Students in the lowest performing group had general deficits in mathematics that were related to intelligence, but above and beyond the effects of intelligence, we observed reliable cognitive differences across clusters. Students in the lowest-performing group had an achievement and cognitive profile that is very similar to that of students identified as having mathematical learning difficulties in the broader literature ( Geary et al., 2007 ; Murphy et al., 2007 ). More precisely, their cognitive profile was characterized by lower intelligence and working memory span (e.g., n-back) than students in other groups, as well as spatial deficits. Interestingly, through Bayesian model comparisons, even though digit span and n-back showed significant main effects, their contribution was mitigated when the effects of other cognitive factors were taken-into-account. This is surprising, as Geary et al. (2012) found especially poor working memory for fifth-graders with a mathematical learning disability, as is commonly found ( Bull & Lee, 2014 ; Mazzocco & Kover, 2007 ; McLean & Hitch, 1999 ). We included a more extensive assessment of cognitive abilities than in most previous studies, including various spatial abilities and spatial working memory. The inclusion of these measures is the most likely explanation for the mitigated contributions of standard working memory measures (e.g., digit span) in differentiating lower-achieving students from their higher achieving peers ( Miyake et al., 2001 ).

The deficits of the lower-performing group, and differences across clusters broadly, were best explained through the combination of intelligence and specific spatial abilities; specifically, visuospatial working memory and visuospatial attention (JLAP). The relationship between mathematics achievement and spatial processing has long been of interest (see Bishop, 1980 for review), and multiple lines of evidence have implicated visuospatial processing in the development of mathematics skills ( Geary, 2004 ; Geer et al., 2019 ; Hawes & Ansari, 2020 ; Mix, 2019 ; Mix et al., 2016, 2017 ; Reuhkala, 2001 ). This might be due to the use of the visuospatial system for representing numerical and mathematical knowledge and implementing certain types of problem-solving strategies, but this is still uncertain ( Hawes & Ansari, 2020 ; Mix, 2019 ).

In any case, Li and Geary (2017) found that the relation between visuospatial working memory and mathematics achievement increases across grades. These types of patterns do not mean there is a casual relationship but if there is (see Gilligan et al., 2020 ), additional deficits in mathematics areas that are influenced by spatial abilities may emerge as students move through middle school and into high school. The results also suggest that incorporating more spatial information into remediation programs could be helpful for struggling students. These could involve short spatial activities that might prime visuospatial attention before the presentation of the mathematical information, as was done by Gilligan and colleagues. Instruction on the use of visuospatial representations to aid in mathematical problem solving, such as word problems, is often helpful ( Hord & Xin, 2013 ). And interventions to improve students’ fractions knowledge and their understanding of equivalence often have spatial components built into them ( Barbieri et al., 2020 ; McNeil et al., 2019 ).

The issue that remains to be determined is whether there is an interaction between student’s spatial abilities and the use of spatial interventions in learning key mathematical concepts. It could be that student’s with strong spatial abilities do not need the same level of spatial scaffolding as their peers which in turn could lead to an underestimate of the importance of these scaffolds in general classroom settings.

Limitations

The correlational nature of the data precludes strong causal statements, and even though all mathematics, attitudinal, and cognitive measures were validated during analysis, the results are largely descriptive. Moreover, students were administered many tasks in an attempt to achieve assessment breadth, but one potential cost is fatigue during the assessments that might have resulted in less-than-optimal performance. Despite these limitations, the assessment of a very large and diverse sample of adolescents across core pre-algebra mathematical competencies and academic attitudes and anxiety provided a broader assessment of mathematical strengths and weaknesses for different subgroups of adolescents than is typical in this literature. Against a background of relatively poor achievement, lower-performing students have an especially poor understanding of mathematical equality and do not fully understand fractions comparisons and how fractions magnitudes map onto the number line. The contribution of the spatial measures to the classification of students into clusters suggests that direct spatial interventions (e.g., Gilligan et al., 2020 ) or the use spatial scaffolds might be useful for the remediation of lower-achieving students’ difficulties with equality and fractions.

Supplementary Material

Acknowledgements:.

The study was supported by grants DRL-1659133 from the National Science Foundation and R01 HD087231 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development and We thank Dana Hibbard of Columbia Public Schools, as well as the staff, faculty, students and families of Columbia Public Schools for their assistance with the logistics of the study. We thank Kristin Balentine, Mandar Bhoyar, Amanda Campbell, Maria Ceriotti, Felicia Chu, Anastasia Compton, Danielle Cooper, Alexis Currie, Kaitlynn Dutzy, Amanda Evans, James Farley, Amy Jordan, Bradley Lance, Kate Leach, Joshua McEwen, Kelly Mebruer, Heather Miller, Natalie Miller, Sarah Peterson, Nicole Reimer, Laura Roider, Brandon Ryffe, Logan Schmidt, Jonathan Thacker, Zehra Unal, and Melissa Willoughby for their assistance with data collection and processing.

Alibali MW, Knuth EJ, Hattikudur S, McNeil NM, & Stephens AC (2007). A longitudinal examination of middle school students’ understanding of the equal sign and equivalent equations. Mathematical Thinking and Learning, 9, 221–247. 10.1080/10986060701360902 [ DOI ] [ Google Scholar ]
Ashcraft MH, & Kirk EP (2001). The relationships among working memory, math anxiety, and performance. Journal of experimental psychology: General, 130, 224–237. 10.1037/0096-3445.130.2.224 [ DOI ] [ PubMed ] [ Google Scholar ]
Barbieri CA, Rodrigues J, Dyson N, & Jordan NC (2020). Improving fraction understanding in sixth graders with mathematics difficulties: Effects of a number line approach combined with cognitive learning strategies. Journal of Educational Psychology, 112, 628–648. 10.1037/edu0000384 [ DOI ] [ Google Scholar ]
Baloglu M, & Koçak R. (2006). A multivariate investigation of the differences in mathematics anxiety. Personality and Individual Differences, 40, 1325–1335. 10.1016/j.paid.2005.10.009 [ DOI ] [ Google Scholar ]
Bartelet D, Ansari D, Vaessen A, & Blomert L. (2014). Cognitive subtypes of mathematics learning difficulties in primary education. Research in Developmental Disabilities, 35, 657–670. 10.1016/j.ridd.2013.12.010 [ DOI ] [ PubMed ] [ Google Scholar ]
Bishop AJ Spatial abilities and mathematics education – A review. Educational Studies in Mathematics, 11, 257–269. 10.1007/BF00697739 [ DOI ] [ Google Scholar ]
Booth JL, Barbieri C, Eyer F, & Paré-Blagoev EJ (2014). Persistent and pernicious errors in algebraic problem solving. The Journal of Problem Solving, 7, 10–23. 10.7771/1932-6246.1161 [ DOI ] [ Google Scholar ]
Booth JL, & Koedinger KR (2008). Key misconceptions in algebraic problem solving. Proceedings of the Annual Meeting of the Cognitive Science Society, 30, 30. Permalink: https://escholarship.org/content/qt5n28t12n/qt5n28t12n.pdf [ Google Scholar ]
Braithwaite DW, Leib ER, Siegler RS, & McMullen J. (2019). Individual differences in fraction arithmetic learning. Cognitive Psychology, 112, 81–98. 10.1016/j.cogpsych.2019.04.002 [ DOI ] [ PubMed ] [ Google Scholar ]
Braithwaite DW, Tian J, & Siegler RS (2018). Do children understand fraction addition? Developmental Science, 21, e12601. 10.1111/desc.12601 [ DOI ] [ PubMed ] [ Google Scholar ]
Bull R, Epsy KA, & Wiebe SA (2008). Short-term memory, working memory, and executive functions in preschoolers: Longitudinal predictors of mathematical achievement at age 7 years. Developmental Neuropsychology, 33, 205–228. 10.1080/87565640801982312 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Bull R, & Lee K. (2014). Executive functioning and mathematics achievement. Child Development Perspectives, 8, 36–41. 10.1111/cdep.12059 [ DOI ] [ Google Scholar ]
Bynner J. (1997). Basic skills in adolescents’ occupational preparation. Career Development Quarterly, 45, 305–321. 10.1002/j.2161-0045.1997.tb00536.x [ DOI ] [ Google Scholar ]
Carey E, Hill F, Devine A, & Szücs D. (2016). The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance. Frontiers in Psychology, 6, 1987. 10.3389/fpsyg.2015.01987 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Carpenter TP, Corbitt MK, Kepner H Jr., Lindquist MM, & Reys R. (1981). Results from the second mathematics assessment of the National Assessment of Educational Progress. Washington, DC: National Council of Teachers of Mathematics. [ Google Scholar ]
Casey BM, Lombardi CM, Pollock A, Fineman B, & Pezaris E. (2017). Girls’ spatial skills and arithmetic strategies in first grade as predictors of fifth-grade analytical math reasoning. Journal of Cognition and Development, 18, 530–555. 10.1080/15248372.2017.1363044 [ DOI ] [ Google Scholar ]
Casey MB, Nuttall R, Pezaris E, & Benbow CP (1995). The influence of spatial ability on gender differences in mathematics college entrance test scores across diverse samples. Developmental Psychology, 31, 697–705. 10.1037/0012-1649.31.4.697 [ DOI ] [ PubMed ] [ Google Scholar ]
Cohen J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Erlbaum. [ Google Scholar ]
Collaer M, Reimers L, & Manning S. (2007). Visuospatial performance on an internet line judgment task and potential hormonal markers: Sex, sexual orientation, and 2D:4D. Archives of Sexual Behavior, 36, 177–192. 10.1007/s10508-006-9152-1 [ DOI ] [ PubMed ] [ Google Scholar ]
Deary IJ, Strand S, Smith P, & Fernandes C. (2007). Intelligence and educational achievement. Intelligence, 35(1), 13–21. 10.1016/j.intell.2006.02.001 [ DOI ] [ Google Scholar ]
De Smedt B, Janssen R, Bouwens K, Verschaffel L, Boets B, & Ghesquière P. (2009). Working memory and individual differences in mathematics achievement: A longitudinal study from first grade to second grade. Journal of Experimental Child Psychology, 103, 186–201. 10.1016/j.jecp.2009.01.004 [ DOI ] [ PubMed ] [ Google Scholar ]
Devine A, Hill F, Carey E, & Szűcs D. (2017). Cognitive and emotional math problems largely dissociate: Prevalence of developmental dyscalculia and mathematics anxiety. Journal of Educational Psychology, 110, 431–444. 10.1037/edu0000222 [ DOI ] [ Google Scholar ]
Dowker A, Sarkar A, & Looi CY (2016). Mathematics Anxiety: What Have We Learned in 60 Years? Frontiers in Psychology, 7, 508. 10.3389/fpsyg.2016.00508 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, ... & Sexton H. (2007). School readiness and later achievement. Developmental Psychology, 43, 1428–1446. 10.1037/0012-1649.43.6.1428 [ DOI ] [ PubMed ] [ Google Scholar ]
Eccles JS, Adler TF, & Meece JL (1984). Sex differences in achievement: A test of alternative theories. Journal of Personality and Social Psychology, 46, 26–43. 10.1037/0022-3514.46.1.26 [ DOI ] [ Google Scholar ]
Eccles JS, & Wang MT (2016). What motivates females and males to pursue careers in mathematics and science? International Journal of Behavioral Development, 40, 100–106. 10.1177/0165025415616201 [ DOI ] [ Google Scholar ]
Eccles JS, & Wigfield A. (2002). Motivational beliefs, values, and goals. Annual Review of Psychology, 53, 109–132. 10.1146/annurev.psych.53.100901.135153 [ DOI ] [ PubMed ] [ Google Scholar ]
Frisco-van den Bos I, van der Ven SH, Kroesbergen EH, & van Luit JE (2013). Working memory and mathematics in primary school children: A meta-analysis. Educational Research Review, 10, 29–44. 10.1111/jcpp.12296 [ DOI ] [ Google Scholar ]
Fuchs LS, Seethaler PM, Sterba SK, Craddock C, Fuchs D. Compton DL, Geary DC & Changas P. (2020). Closing the word-problem achievement gap in first grade: Schema-based word-problem intervention with embedded language comprehension instruction. Journal of Educational Psychology. Advance online doi. 10.10.1037/edu000046 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Geary DC (2004). Mathematics and learning disabilities. Journal of Learning Disabilities, 37, 4–15. 10.1177/00222194040370010201 [ DOI ] [ PubMed ] [ Google Scholar ]
Geary DC (2011). Cognitive predictors of individual differences in achievement growth in mathematics: A five-year longitudinal study. Developmental Psychology, 47, 1539–1552. 10.1037/a0025510 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Geary DC, Hoard MK, Byrd-Craven J, Nugent L, & Numtee C. (2007). Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development, 78, 1343–1359. 10.1111/j.1467-8624.2007.01069.x [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Geary DC, Hoard MK, Nugent L, & Bailey DH (2012). Mathematical cognition deficits in children with learning disabilities and persistent low achievement: A five-year prospective study. Journal of Educational Psychology, 104, 206–223. 10.1037/a0025398 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Geary DC, Hoard MK, Nugent L, & Bailey HD (2013). Adolescents’ functional numeracy is predicted by their school entry number system knowledge. PLoS ONE, 8: e54651. 10.1371/journal.pone.0054651 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Geary DC, Hoard MK, Nugent L, Chu FW, Scofield JE, & Hibbard DF (2019). Sex differences in mathematics anxiety and attitudes: Concurrent and longitudinal relations to mathematical competence. Journal of Educational Psychology. 111(8), 1447–1461. 10.1037/edu0000355. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Geary DC, Scofield JE, Hoard MK, & Nugent L. (2020). Boys’ advantage on the fractions number line is mediated by visuospatial attention: Evidence for a parietal-spatial contribution to number line learning. Developmental Science. Advance Online doi 10.1111/desc.13063. [ DOI ] [ PubMed ] [ Google Scholar ]
Geary DC, Nicholas A, Li Y, & Sun J. (2017). Developmental change in the influence of domain-general abilities and domain-specific knowledge on mathematics achievement: An eight-year longitudinal study. Journal of Educational Psychology, 109, 680–693. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Geary DC, & Widaman KF (1992). Numerical cognition: On the convergence of componential and psychometric models. Intelligence, 16, 47–80. 10.1016/0160-2896(92)90025-M [ DOI ] [ Google Scholar ]
Geer EA, Quinn JM, & Ganley CM (2019). Relations between spatial skills and math performance in elementary school children: A longitudinal investigation. Developmental Psychology, 55, 637–652. 10.1037/dev0000649 [ DOI ] [ PubMed ] [ Google Scholar ]
Gignac GE, & Zajenkowski M. (2020). The Dunning-Kruger effect is (mostly) a statistical artefact: Valid approaches to testing the hypothesis with individual differences data. Intelligence, 80, 101449. 10.1016/j.intell.2020.101449 [ DOI ] [ Google Scholar ]
Gilligan KA, Thomas MS, & Farran EK (2020). First demonstration of effective spatial training for near transfer to spatial performance and far transfer to a range of mathematics skills at 8 years. Developmental Science, 23, e12909. 10.1111/desc.12909\ [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Gunderson EA, Park D, Maloney EA, Beilock SL, & Levine SC (2018). Reciprocal relations among motivational frameworks, math anxiety, and math achievement in early elementary school. Journal of Cognition and Development, 19, 21–46. 10.1080/15248372.2017.1421538 [ DOI ] [ Google Scholar ]
Hawes Z, & Ansari D. (2020). What explains the relationship between spatial and mathematical skills? A review of evidence from brain and behavior. Psychonomic Bulletin & Review, 27, 465–482. 10.3758/s13423-019-01694-7 [ DOI ] [ PubMed ] [ Google Scholar ]
Hecht SA, & Vagi KJ (2010). Sources of group and individual differences in emerging fraction skills. Journal of Educational Psychology, 102, 843–859. 10.1037/a0019824 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Hembree R. (1990). The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education, 21, 33–46. 10.2307/749455 [ DOI ] [ Google Scholar ]
Hennig C. (2007). Cluster-wise assessment of cluster stability. Computational Statistics & Data Analysis, 52(1), 258–271. 10.1016/j.csda.2006.11.025 [ DOI ] [ Google Scholar ]
Hill F, Mammarella IC, Devine A, Caviola S, Passolunghi MC, & Szűcs D. (2016). Maths anxiety in primary and secondary school students: Gender differences, developmental changes and anxiety specificity. Learning and Individual Differences, 48, 45–53. 10.1016/j.lindif.2016.02.006 [ DOI ] [ Google Scholar ]
Hopko DR, Mahadevan R, Bare RL, & Hunt MK (2003). The abbreviated math anxiety scale (AMAS) construction, validity, and reliability. Assessment, 10, 178–182. 10.1177/1073191103010002008 [ DOI ] [ PubMed ] [ Google Scholar ]
Hord C, & Xin YP (2013). Intervention research for helping elementary school students with math learning difficulties understand and solve word problems: 1996–2010. Learning Disabilities, 19, 3–17. 10.18666/LDMJ-2013-V19-I1-4789 [ DOI ] [ Google Scholar ]
Jaeggi SM, Studer-Luethi B, Buschkuehl M, Su Y-F, Jonides J, & Perrig WJ (2010). The relationship between n-back performance and matrix reasoning—Implications for training and transfer. Intelligence, 38(6), 625–635. 10.1016/j.intell.2010.09.001 [ DOI ] [ Google Scholar ]
Jansen RA, Rafferty AN, & Griffiths TL (2021). A rational model of the Dunning–Kruger effect supports insensitivity to evidence in low performers. Nature Human Behaviour, 1–8. 10.1038/s41562-021-01057-0 [ DOI ] [ PubMed ] [ Google Scholar ]
Kass RE, & Raftery AE (1995). Bayes factors. Journal of the American Statistical Association, 90(430), 773–795. 10.1080/01621459.1995.10476572 [ DOI ] [ Google Scholar ]
Kell HJ, Lubinski D, Benbow CP, & Steiger JH (2013). Creativity and technical innovation: Spatial ability’s unique role. Psychological Science, 24, 1831–1836. 10.1177/0956797613478615 [ DOI ] [ PubMed ] [ Google Scholar ]
Kessels RPC, van Zandvoort MJE, Postma A, Kappelle LJ, & de Haan EHF (2000). The Corsi block-tapping task: Standardization and normative data. Applied Neuropsychology, 7(4), 252–258. 10.1207/S15324826AN0704_8 [ DOI ] [ PubMed ] [ Google Scholar ]
Knuth EJ, Alibali MW, McNeil NM, Weinberg A, & Stephens AC (2005). Middle school students’ understanding of core algebraic concepts: Equivalence & variable. Zentralblatt für Didaktik der Mathematik (International Reviews on Mathematics Education), 37, 68–76. 10.1007/BF02655899.ris [ DOI ] [ Google Scholar ]
Kruger J, & Dunning D. (1999). Unskilled and unaware of it: how difficulties in recognizing one’s own incompetence lead to inflated self-assessments. Journal of Personality and Social Psychology, 77, 1121–1134. 10.1037/0022-3514.77.6.1121 [ DOI ] [ PubMed ] [ Google Scholar ]
Kyttälä M, & Lehto JE (2008). Some factors underlying mathematical performance: The role of visuospatial working memory and non-verbal intelligence. European Journal of Psychology of Education, 23, 77–94. 10.1007/BF03173141 [ DOI ] [ Google Scholar ]
Lauermann F, Tsai YM, & Eccles JS (2017). Math-related career aspirations and choices within Eccles et al.’s expectancy–value theory of achievement-related behaviors. Developmental Psychology, 53, 1540–1559. 10.1037/dev0000367 [ DOI ] [ PubMed ] [ Google Scholar ]
Li Y, & Geary DC (2017). Children’s visuospatial memory predicts mathematics achievement through early adolescence. PLoS ONE, 12(2): e0172046. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Longo MR, & Lourenco SF (2007). Spatial attention and the mental number line: Evidence for characteristic biases and compression. Neuropsychologia, 45, 1400–1407. doi: 10.1016/j.neuropsychologia.2006.11.002 [ DOI ] [ PubMed ] [ Google Scholar ]
Maloney EA, & Beilock SL (2012). Math anxiety: who has it, why it develops, and how to guard against it. Trends in Cognitive Sciences, 16, 404–406. 10.1016/j.tics.2012.06.008 [ DOI ] [ PubMed ] [ Google Scholar ]
Mamedova S, Sparks D, & Hoyer KM (2017). Adult education attainment and assessment scores: A cross-national comparison. (NCES 2018–007). Washington, DC: National Center for Education Statistics. [ Google Scholar ]
Martin WG, Strutchens ME, & Elliott PC (2007). The learning of mathematics. Reston, VA: National Council of Teachers of Mathematics. [ Google Scholar ]
Mazzocco M, & Devlin KT (2008). Parts and holes: Gaps in rational number sense in children with vs. without mathematical learning disability. Developmental Science, 11, 681–691. 10.1111/j.1467-7687.2008.00717.x [ DOI ] [ PubMed ] [ Google Scholar ]
Mazzocco MMM, & Kover ST (2007). A longitudinal assessment of executive function skills and their association with math performance. Child Neuropsychology, 13, 18–45. 10.1080/09297040600611346 [ DOI ] [ PubMed ] [ Google Scholar ]
McIntosh RD, Fowler EA, Lyu T, & Della Sala S. (2019). Wise up: Clarifying the role of metacognition in the Dunning-Kruger effect. Journal of Experimental Psychology: General, 148, 1882–1897. 10.1037/xge0000579 [ DOI ] [ PubMed ] [ Google Scholar ]
Meece JL, Wigfield A, & Eccles JS (1990). Predictors of math anxiety and its influence on young adolescents’ course enrollment intentions and performance in mathematics. Journal of Educational Psychology, 82, 60–70. 10.1037/0022-0663.82.1.60 [ DOI ] [ Google Scholar ]
McNeil NM, Hornburg CB, Devlin BL, Carrazza C, & McKeever MO (2019). Consequences of individual differences in children’s formal understanding of mathematical equivalence. Child Development, 90, 940–956. 10.1111/cdev.12948 [ DOI ] [ PubMed ] [ Google Scholar ]
McLean JF, & Hitch GJ (1999). Working memory impairments in children with specific arithmetic learning difficulties. Journal of Experimental Child Psychology, 74, 240–260. 10.1006/jecp.1999.2516 [ DOI ] [ PubMed ] [ Google Scholar ]
McNeil NM, Fyfe ER, Petersen LA, Dunwiddie AE, & Brletic-Shipley H. (2011). Benefits of practicing 4= 2+ 2: Nontraditional problem formats facilitate children’s understanding of mathematical equivalence. Child Development, 82, 1620–1633. 10.1111/j.1467-8624.2011.01622.x [ DOI ] [ PubMed ] [ Google Scholar ]
Mix KS (2019). Why are spatial skill and mathematics related? Child Development Perspectives, 13, 121–126. 10.1111/cdep12323 [ DOI ] [ Google Scholar ]
Mix KS, & Cheng YL (2012). The relation between space and math: Developmental and educational implications. Advances in Child Development and Behavior, 42, 197–243. 10.1016/B978-0-12-394388-0.00006-X [ DOI ] [ PubMed ] [ Google Scholar ]
Mix KS, Levine SC, Cheng YL, Young CJ, Hambrick DZ, & Konstantopoulos S. (2017). The latent structure of spatial skills and mathematics: A replication of the two-factor model. Journal of Cognition and Development, 18, 465–492. doi: 10.1080/15248372.2017.1346658 [ DOI ] [ Google Scholar ]
Miyake A, Friedman NP, Emerson MJ, Witzki AH, Howerter A, & Wager TD (2000). The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis. Cognitive Psychology, 41, 49–100. 10.1006/cogp.1999.0734 [ DOI ] [ PubMed ] [ Google Scholar ]
Miyake A, Friedman NP, Rettinger DA, Shah P, & Hegarty M. (2001). How are visuospatial working memory, executive functioning, and spatial abilities related? A latent-variable analysis. Journal of Experimental Psychology: General, 130, 621–640. 10.1037//0096-3445.130.4.621 [ DOI ] [ PubMed ] [ Google Scholar ]
Murphy MM, Mazzocco MM, Hanich LB, & Early MC (2007). Cognitive characteristics of children with mathematics learning disability (MLD) vary as a function of the cutoff criterion used to define MLD. Journal of Learning Disabilities, 40, 458–478. 10.1177/00222194070400050901 [ DOI ] [ PubMed ] [ Google Scholar ]
National Mathematics Advisory Panel. (2008). Foundations for Success: Final Report of the National Mathematics Advisory Panel. Washington, DC: United States Department of Education. http://www.ed.gov/about/bdscomm/list/mathpanel/report/final-report.pdf [ Google Scholar ]
Peters M, Laeng B, Latham K, Jackson M, Zaiyouna R, & Richardson C. (1995). A redrawn Vandenberg and Kuse mental rotations test: Different versions and factors that affect performance. Brain and Cognition, 28, 39–58. 10.1006/brcg.1995.1032 [ DOI ] [ PubMed ] [ Google Scholar ]
R Core Team. (2017). R: A language and environment for statistical computing. Retrieved from https://www.R-project.org/
Reuhkala M. (2001). Mathematical skills in ninth-graders: Relationship with visuo-spatial abilities and working memory. Educational Psychology, 21(4), 387–399. 10.1080/01443410120090786 [ DOI ] [ Google Scholar ]
Reyna VF, Nelson WL, Han PK, & Dieckmann NF (2009). How numeracy influences risk comprehension and medical decision making. Psychological Bulletin, 135, 943–973. 10.1037/a0017327 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Ritchie SJ, & Bates TC (2013). Enduring links from childhood mathematics and reading achievement to adult socioeconomic status. Psychological Science, 24, 1301–1308. 10.1177/0956797612466268 [ DOI ] [ PubMed ] [ Google Scholar ]
Rouder JN, Engelhardt CR, McCabe S, & Morey RD (2016). Model comparison in ANOVA. Psychonomic Bulletin & Review, 23(6), 1779–1786. 10.3758/s13423-016-1026-5 [ DOI ] [ PubMed ] [ Google Scholar ]
SAS Institute. (2014). Statistical analysis system 9.2. Cary, NC: Author. [ Google Scholar ]
Siegler RS, Duncan GJ, Davis-Kean PE, Duckworth K, Claessens A, Engel M, … & Chen M. (2012). Early predictors of high school mathematics achievement. Psychological Science, 23, 691–697. 10.1177/0956797612440101 [ DOI ] [ PubMed ] [ Google Scholar ]
Siegler RS, Thompson CA, & Schneider M. (2011). An integrated theory of whole number and fractions development. Cognitive Psychology, 62, 273–296. 10.1016/j.cogpsych.2011.03.001 [ DOI ] [ PubMed ] [ Google Scholar ]
Swanson HL, Jerman O, & Zheng X. (2008). Growth in working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology, 100, 343–379. 10.1037/0022-0663.100.2.343 [ DOI ] [ Google Scholar ]
Sweller J, van Merriënboer JJ, & Paas F. (2019). Cognitive architecture and instructional design: 20 years later. Educational Psychology Review, 31, 261–292. 10.1007/s10648-019-09465-5 [ DOI ] [ Google Scholar ]
Talsma K, Schüz B, Schwarzer R, & Norris K. (2018). I believe, therefore I achieve (and vice versa): A meta-analytic cross-lagged panel analysis of self-efficacy and academic performance. Learning and Individual Differences, 61, 136–150. 10.1016/j.lindif.2017.11.015 [ DOI ] [ Google Scholar ]
Tolar TD, Lederberg AR, & Fletcher JM (2009). A structural model of algebra achievement: computational fluency and spatial visualisation as mediators of the effect of working memory on algebra achievement. Educational Psychology, 29, 239–266. 10.1080/01443410802708903 [ DOI ] [ Google Scholar ]
Van de Weijer-Bergsma E, Kroesbergen EH, & Van Luit JE (2015). Verbal and visual-spatial working memory and mathematical ability in different domains throughout primary school. Memory & Cognition, 43, 367–378. 10.3758/s13421-014-0480-4 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Valentine JC, DuBois DL, & Cooper H. (2004). The relation between self-beliefs and academic achievement: A meta-analytic review. Educational Psychologist, 39, 111–133. 10.1207/s15326985ep3902_3 [ DOI ] [ Google Scholar ]
Valentine KD, Buchanan EM, Scofield JE, & Beauchamp MT (2019). Beyond p values: Utilizing multiple methods to evaluate evidence. Behaviormetrika, 46(1), 121–144. 10.1007/s41237-019-00078-4 [ DOI ] [ Google Scholar ]
Vanbinst K, Ceulemans E, Ghesquière P, De Smedt B. (2015). Profiles of children’s arithmetic fact development: A model-based clustering approach. Journal of Experimental Child Psychology, 133, 29–46. 10.1016/j.jecp.2015.01.0030022-0965 [ DOI ] [ PubMed ] [ Google Scholar ]
Wechsler D. (1999). Wechsler Abbreviated Scale of Intelligence. San Antonio, TX: PsychCorp, Harcourt Assessment, Inc. [ Google Scholar ]
Wechsler D. (2009). Wechsler Individual Achievement Test (3rd ed.). San Antonio, TX: Psychological Corporation. [ Google Scholar ]
Woods DL, Kishiyama MM, Yund EW, Herron TJ, Edwards B, Poliva O, … and Reed B. (2011). Improving digit span assessment of short-term verbal memory. Journal of Clinical and Experimental Neuropsychology, 33(1), 101–111. 10.1080/13803395.2010.493149 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
Zorzi M, Bonato M, Treccani B, Scalambrin G, Marenzi R, & Priftis K. (2012). Neglect impairs explicit processing of the mental number line. Frontiers in Human Neuroscience, 6, 125. doi: 10.3389/fnhum.2012.00125 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

View on publisher site
PDF (1.1 MB)
Collections

Add to Collections

IMAGES

Strengths and Weaknesses Free Essay Example
Academic Strength and Weakness Free Essay Example 279 words
≫ Beating my Weaknesses Free Essay Sample on Samploon.com
5 Tips to Overcome Weakness in Math and score 100 in CBSE Class 10 Board Exams @VedantuClass9_10_11
Mathematics In Everyday Life: Most Vital Discipline: [Essay Example
Understanding Your Strengths And Weaknesses Free Essay Example

VIDEO

math is my weakness #furry #therianthropy #mathsucks
The biggest MYTH in math 😳
Should Math Books Include Solutions? My Opinion
Sigma math teacher Mr bean 🗿 #remixermedul #sigma #mathteacher #sigmamath #mrbeast
9th Class Test Topper I MathZone Short Video
Likely BECE 2025 Mathematics Questions & Answers

COMMENTS

Reflection On Strengths And Weaknesses In Mathematics (Free ...
Reflecting on these strengths and weaknesses has highlighted the importance of self-awareness in academic pursuit. Mathematics is a discipline that demands both natural aptitude and...
My Weakness In Math - 740 Words | Internet Public Library
My Weakness In Math. 740 Words3 Pages. When I think about myself, as a math learner one thing that I know is very important is low stress. Growing up during Elementary school, Middle school and high school I always enjoyed math and found it to be a very interesting and relaxing subject.
Mathematics Difficulties - All Kinds of Minds
Math difficulties can arise at nearly any stage of a child’s scholastic development. While very little is known about the neurobiological or environmental causes of these problems, many experts attribute them to weaknesses in one or more of the skill types listed below.
My Academic Strengths And Academic Weaknesses: [Essay Example ...
Understanding these strengths and weaknesses is crucial for personal growth and development. In this essay, I will explore my academic strengths and weaknesses, highlighting how they have influenced my educational journey and discussing the implications of these strengths and weaknesses.
Reflection On Strengths And Weaknesses In Mathematics
In the story “Why is Math so important for kids to learn?” by Elise Wile, the author’s attitude toward Math is interested for these reasons: (1) she explains how it teaches logical and critical thinking, (2) she explains how it teaches life skills, and (3) she also explains how it supports continuing education and careers.…
The Top 5 Reasons Students Struggle With Math - Tutor Doctor
So, if you’re out there wondering, “why do I struggle with math so much?” there may be a number of reasons, from attention difficulties to learning gaps from past math classes or even just lack of practice. Take a look at common reasons students struggle with math, and how to find the right help you need to succeed.
Comparison Of My Math Strengths And Weaknesses
My Math Strengths and Weaknesses. As I am approaching the end of my educational career, it is time for me to evaluate how well I will do teaching a subject I struggled in elementary school, math. Math is a subject I had a love hate relationship with.
Mathematics Clusters Reveal Strengths and Weaknesses in ...
If mathematics attitudes or anxiety are associated with specific clusters of pre-algebra strengths and weaknesses, they could exacerbate or ameliorate at-risk students’ engagement in middle-school mathematics and thus their preparation for algebra.
TEACHER NOTICING STUDENTS’ MATHEMATICAL STRENGTHS - ed
r how to notice students’ mathematical strengths. The lens on strengths runs counter to the prevalent culture in U.S. schools. o overemphasize gaps in students’ understandings. In this paper we describe a video club focused on identifying and naming students’ mathematical.
MATHEMATICS PHOBIA: CAUSES, SYMPTOMS AND WAYS TO OVERCOME
The main causes of mathematics phobia include test and examination, individuals, teachers, parents, peers and the nature of mathematics. The only ways to overcome mathematics phobia, is the ...