computer programming problem solving process

What Is Problem Solving? How Software Engineers Approach Complex Challenges

From debugging an existing system to designing an entirely new software application, a day in the life of a software engineer is filled with various challenges and complexities. The one skill that glues these disparate tasks together and makes them manageable? Problem solving . 

Throughout this blog post, we’ll explore why problem-solving skills are so critical for software engineers, delve into the techniques they use to address complex challenges, and discuss how hiring managers can identify these skills during the hiring process. 

What Is Problem Solving?

But what exactly is problem solving in the context of software engineering? How does it work, and why is it so important?

Problem solving, in the simplest terms, is the process of identifying a problem, analyzing it, and finding the most effective solution to overcome it. For software engineers, this process is deeply embedded in their daily workflow. It could be something as simple as figuring out why a piece of code isn’t working as expected, or something as complex as designing the architecture for a new software system. 

In a world where technology is evolving at a blistering pace, the complexity and volume of problems that software engineers face are also growing. As such, the ability to tackle these issues head-on and find innovative solutions is not only a handy skill — it’s a necessity. 

The Importance of Problem-Solving Skills for Software Engineers

Problem-solving isn’t just another ability that software engineers pull out of their toolkits when they encounter a bug or a system failure. It’s a constant, ongoing process that’s intrinsic to every aspect of their work. Let’s break down why this skill is so critical.

Driving Development Forward

Without problem solving, software development would hit a standstill. Every new feature, every optimization, and every bug fix is a problem that needs solving. Whether it’s a performance issue that needs diagnosing or a user interface that needs improving, the capacity to tackle and solve these problems is what keeps the wheels of development turning.

It’s estimated that 60% of software development lifecycle costs are related to maintenance tasks, including debugging and problem solving. This highlights how pivotal this skill is to the everyday functioning and advancement of software systems.

Innovation and Optimization

The importance of problem solving isn’t confined to reactive scenarios; it also plays a major role in proactive, innovative initiatives . Software engineers often need to think outside the box to come up with creative solutions, whether it’s optimizing an algorithm to run faster or designing a new feature to meet customer needs. These are all forms of problem solving.

Consider the development of the modern smartphone. It wasn’t born out of a pre-existing issue but was a solution to a problem people didn’t realize they had — a device that combined communication, entertainment, and productivity into one handheld tool.

Increasing Efficiency and Productivity

Good problem-solving skills can save a lot of time and resources. Effective problem-solvers are adept at dissecting an issue to understand its root cause, thus reducing the time spent on trial and error. This efficiency means projects move faster, releases happen sooner, and businesses stay ahead of their competition.

Improving Software Quality

Problem solving also plays a significant role in enhancing the quality of the end product. By tackling the root causes of bugs and system failures, software engineers can deliver reliable, high-performing software. This is critical because, according to the Consortium for Information and Software Quality, poor quality software in the U.S. in 2022 cost at least $2.41 trillion in operational issues, wasted developer time, and other related problems.

Problem-Solving Techniques in Software Engineering

So how do software engineers go about tackling these complex challenges? Let’s explore some of the key problem-solving techniques, theories, and processes they commonly use.

Decomposition

Breaking down a problem into smaller, manageable parts is one of the first steps in the problem-solving process. It’s like dealing with a complicated puzzle. You don’t try to solve it all at once. Instead, you separate the pieces, group them based on similarities, and then start working on the smaller sets. This method allows software engineers to handle complex issues without being overwhelmed and makes it easier to identify where things might be going wrong.

Abstraction

In the realm of software engineering, abstraction means focusing on the necessary information only and ignoring irrelevant details. It is a way of simplifying complex systems to make them easier to understand and manage. For instance, a software engineer might ignore the details of how a database works to focus on the information it holds and how to retrieve or modify that information.

Algorithmic Thinking

At its core, software engineering is about creating algorithms — step-by-step procedures to solve a problem or accomplish a goal. Algorithmic thinking involves conceiving and expressing these procedures clearly and accurately and viewing every problem through an algorithmic lens. A well-designed algorithm not only solves the problem at hand but also does so efficiently, saving computational resources.

Parallel Thinking

Parallel thinking is a structured process where team members think in the same direction at the same time, allowing for more organized discussion and collaboration. It’s an approach popularized by Edward de Bono with the “ Six Thinking Hats ” technique, where each “hat” represents a different style of thinking.

In the context of software engineering, parallel thinking can be highly effective for problem solving. For instance, when dealing with a complex issue, the team can use the “White Hat” to focus solely on the data and facts about the problem, then the “Black Hat” to consider potential problems with a proposed solution, and so on. This structured approach can lead to more comprehensive analysis and more effective solutions, and it ensures that everyone’s perspectives are considered.

This is the process of identifying and fixing errors in code . Debugging involves carefully reviewing the code, reproducing and analyzing the error, and then making necessary modifications to rectify the problem. It’s a key part of maintaining and improving software quality.

Testing and Validation

Testing is an essential part of problem solving in software engineering. Engineers use a variety of tests to verify that their code works as expected and to uncover any potential issues. These range from unit tests that check individual components of the code to integration tests that ensure the pieces work well together. Validation, on the other hand, ensures that the solution not only works but also fulfills the intended requirements and objectives.

Explore verified tech roles & skills.

The definitive directory of tech roles, backed by machine learning and skills intelligence.

Explore all roles

Evaluating Problem-Solving Skills

We’ve examined the importance of problem-solving in the work of a software engineer and explored various techniques software engineers employ to approach complex challenges. Now, let’s delve into how hiring teams can identify and evaluate problem-solving skills during the hiring process.

Recognizing Problem-Solving Skills in Candidates

How can you tell if a candidate is a good problem solver? Look for these indicators:

• Previous Experience: A history of dealing with complex, challenging projects is often a good sign. Ask the candidate to discuss a difficult problem they faced in a previous role and how they solved it.
• Problem-Solving Questions: During interviews, pose hypothetical scenarios or present real problems your company has faced. Ask candidates to explain how they would tackle these issues. You’re not just looking for a correct solution but the thought process that led them there.
• Technical Tests: Coding challenges and other technical tests can provide insight into a candidate’s problem-solving abilities. Consider leveraging a platform for assessing these skills in a realistic, job-related context.

Assessing Problem-Solving Skills

Once you’ve identified potential problem solvers, here are a few ways you can assess their skills:

• Solution Effectiveness: Did the candidate solve the problem? How efficient and effective is their solution?
• Approach and Process: Go beyond whether or not they solved the problem and examine how they arrived at their solution. Did they break the problem down into manageable parts? Did they consider different perspectives and possibilities?
• Communication: A good problem solver can explain their thought process clearly. Can the candidate effectively communicate how they arrived at their solution and why they chose it?
• Adaptability: Problem-solving often involves a degree of trial and error. How does the candidate handle roadblocks? Do they adapt their approach based on new information or feedback?

Hiring managers play a crucial role in identifying and fostering problem-solving skills within their teams. By focusing on these abilities during the hiring process, companies can build teams that are more capable, innovative, and resilient.

Key Takeaways

As you can see, problem solving plays a pivotal role in software engineering. Far from being an occasional requirement, it is the lifeblood that drives development forward, catalyzes innovation, and delivers of quality software. 

By leveraging problem-solving techniques, software engineers employ a powerful suite of strategies to overcome complex challenges. But mastering these techniques isn’t simple feat. It requires a learning mindset, regular practice, collaboration, reflective thinking, resilience, and a commitment to staying updated with industry trends. 

For hiring managers and team leads, recognizing these skills and fostering a culture that values and nurtures problem solving is key. It’s this emphasis on problem solving that can differentiate an average team from a high-performing one and an ordinary product from an industry-leading one.

At the end of the day, software engineering is fundamentally about solving problems — problems that matter to businesses, to users, and to the wider society. And it’s the proficient problem solvers who stand at the forefront of this dynamic field, turning challenges into opportunities, and ideas into reality.

This article was written with the help of AI. Can you tell which parts?

Get started with HackerRank

Over 2,500 companies and 40% of developers worldwide use HackerRank to hire tech talent and sharpen their skills.

Problem Solving

Solving problems is the core of computer science. Programmers must first understand how a human solves a problem, then understand how to translate this "algorithm" into something a computer can do, and finally how to "write" the specific syntax (required by a computer) to get the job done. It is sometimes the case that a machine will solve a problem in a completely different way than a human.

Computer Programmers are problem solvers. In order to solve a problem on a computer you must:

Know how to represent the information (data) describing the problem.

Determine the steps to transform the information from one representation into another.

Information Representation

A computer, at heart, is really dumb. It can only really know about a few things... numbers, characters, booleans, and lists (called arrays) of these items. (See Data Types). Everything else must be "approximated" by combinations of these data types.

A good programmer will "encode" all the "facts" necessary to represent a problem in variables (See Variables). Further, there are "good ways" and "bad ways" to encode information. Good ways allow the computer to easily "compute" new information.

An algorithm (see Algorithm) is a set of specific steps to solve a problem. Think of it this way: if you were to tell your 3 year old neice to play your favorite song on the piano (assuming the neice has never played a piano), you would have to tell her where the piano was, and how to sit on the bench, and how to open the cover, and which keys to press, and which order to press them in, etc, etc, etc.

The core of what good programmers do is being able to define the steps necessary to accomplish a goal. Unfortunately, a computer, only knows a very restricted and limited set of possible steps. For example a computer can add two numbers. But if you want to find the average of two numbers, this is beyond the basic capabilities of a computer. To find the average, you must:

• First: Add the two numbers and save this result in a variable
• Then: Divide this new number the number two, and save this result in a variable.
• Finally: provide this number to the rest of the program (or print it for the user).

We "compute" all the time. Computing is the act of solving problems (or coming up with a plan to solve problems) in an organized manner. We don't need computers to "compute". We can use our own brain.

Encapsulation and Abstraction and Complexity Hiding

Computer scientists like to use the fancy word "Encapsulation" to show how smart we are. This is just a term for things we do as humans every day. It is combined with another fancy term: "Abstraction".

Abstraction is the idea of "ignoring the details". For example, a forest is really a vastly complex ecosystem containing trees, animals, water paths, etc, etc, etc. But to a computer scientist (and to a normal person), its just "a forest".

For example, if your professor needs a cup of coffee, and asks you the single item: "Get me a cup of coffee", he has used both encapsulation and abstraction. The number of steps required to actually get the coffee are enumerable. Including, getting up, walking down the hall, getting in your car, driving to a coffee stand, paying for the coffee, etc, etc, etc. Further, the idea of what a cup of coffee is, is abstract. Do you bring a mug of coffee, or a Styrofoam cup? Is it caffeinated or not? Is it freshly brewed or from concentrate? Does it come from Africa or America?

All of this information is TOO MUCH and we would quickly be unable to funciton if we had to remember all of these details. Thus we "abstract away" the details and only remember the few important items.

This brings us to the idea of "Complexity Hiding". Complexity hiding is the idea that most of the times details don't matter. In a computer program, as simple an idea as drawing a square on the screen involves hundreds (if not thousands) of (low level) computer instructions. Again, a person couldn't possible create interesting programs if every time they wanted to do something, they had to re-write (correctly) every one of those instructions. By "ecapsulating" what is meant by "draw square" and "reusing" this operation over and over again, we make programming tractable.

Encapsulation

The idea behind encapsulation is to store the information necessary to a particular idea in a set of variables associated with a single "object". We then create functions to manipulate this object, regardless of what the actual data is. From that point on, we treat the idea from a "high level" rather than worry about all the parts (data) and actions (functions) necessary to represent the object in a computer.

Brute Force

Brute force is a technique for solving problems that relies on a computers speed (how fast it can repeat steps) to solve a problem. For example, if you wanted to know how many times the number 8 goes into the number 100, you could do the following:

Of course this is a silly way for a computer (or a human) to solve this problem. The real way we would do it is:

When in doubt, you can often use "brute force" to solve a problem, but it often saves time (at least computer time) to think about the problem and solve it in an elegant manner.

How to think like a programmer — lessons in problem solving

By Richard Reis

If you’re interested in programming, you may well have seen this quote before:

“Everyone in this country should learn to program a computer, because it teaches you to think.” — Steve Jobs

You probably also wondered what does it mean, exactly, to think like a programmer? And how do you do it??

Essentially, it’s all about a more effective way for problem solving .

In this post, my goal is to teach you that way.

By the end of it, you’ll know exactly what steps to take to be a better problem-solver.

Why is this important?

Problem solving is the meta-skill.

We all have problems. Big and small. How we deal with them is sometimes, well…pretty random.

Unless you have a system, this is probably how you “solve” problems (which is what I did when I started coding):

• Try a solution.
• If that doesn’t work, try another one.
• If that doesn’t work, repeat step 2 until you luck out.

Look, sometimes you luck out. But that is the worst way to solve problems! And it’s a huge, huge waste of time.

The best way involves a) having a framework and b) practicing it.

“Almost all employers prioritize problem-solving skills first. Problem-solving skills are almost unanimously the most important qualification that employers look for….more than programming languages proficiency, debugging, and system design. Demonstrating computational thinking or the ability to break down large, complex problems is just as valuable (if not more so) than the baseline technical skills required for a job.” — Hacker Rank ( 2018 Developer Skills Report )

Have a framework

To find the right framework, I followed the advice in Tim Ferriss’ book on learning, “ The 4-Hour Chef ”.

It led me to interview two really impressive people: C. Jordan Ball (ranked 1st or 2nd out of 65,000+ users on Coderbyte ), and V. Anton Spraul (author of the book “ Think Like a Programmer: An Introduction to Creative Problem Solving ”).

I asked them the same questions, and guess what? Their answers were pretty similar!

Soon, you too will know them.

Sidenote: this doesn’t mean they did everything the same way. Everyone is different. You’ll be different. But if you start with principles we all agree are good, you’ll get a lot further a lot quicker.

“The biggest mistake I see new programmers make is focusing on learning syntax instead of learning how to solve problems.” — V. Anton Spraul

So, what should you do when you encounter a new problem?

Here are the steps:

1. Understand

Know exactly what is being asked. Most hard problems are hard because you don’t understand them (hence why this is the first step).

How to know when you understand a problem? When you can explain it in plain English.

Do you remember being stuck on a problem, you start explaining it, and you instantly see holes in the logic you didn’t see before?

Most programmers know this feeling.

This is why you should write down your problem, doodle a diagram, or tell someone else about it (or thing… some people use a rubber duck ).

“If you can’t explain something in simple terms, you don’t understand it.” — Richard Feynman

Don’t dive right into solving without a plan (and somehow hope you can muddle your way through). Plan your solution!

Nothing can help you if you can’t write down the exact steps.

In programming, this means don’t start hacking straight away. Give your brain time to analyze the problem and process the information.

To get a good plan, answer this question:

“Given input X, what are the steps necessary to return output Y?”

Sidenote: Programmers have a great tool to help them with this… Comments!

Pay attention. This is the most important step of all.

Do not try to solve one big problem. You will cry.

Instead, break it into sub-problems. These sub-problems are much easier to solve.

Then, solve each sub-problem one by one. Begin with the simplest. Simplest means you know the answer (or are closer to that answer).

After that, simplest means this sub-problem being solved doesn’t depend on others being solved.

Once you solved every sub-problem, connect the dots.

Connecting all your “sub-solutions” will give you the solution to the original problem. Congratulations!

This technique is a cornerstone of problem-solving. Remember it (read this step again, if you must).

“If I could teach every beginning programmer one problem-solving skill, it would be the ‘reduce the problem technique.’ For example, suppose you’re a new programmer and you’re asked to write a program that reads ten numbers and figures out which number is the third highest. For a brand-new programmer, that can be a tough assignment, even though it only requires basic programming syntax. If you’re stuck, you should reduce the problem to something simpler. Instead of the third-highest number, what about finding the highest overall? Still too tough? What about finding the largest of just three numbers? Or the larger of two? Reduce the problem to the point where you know how to solve it and write the solution. Then expand the problem slightly and rewrite the solution to match, and keep going until you are back where you started.” — V. Anton Spraul

By now, you’re probably sitting there thinking “Hey Richard... That’s cool and all, but what if I’m stuck and can’t even solve a sub-problem??”

First off, take a deep breath. Second, that’s fair.

Don’t worry though, friend. This happens to everyone!

The difference is the best programmers/problem-solvers are more curious about bugs/errors than irritated.

In fact, here are three things to try when facing a whammy:

• Debug: Go step by step through your solution trying to find where you went wrong. Programmers call this debugging (in fact, this is all a debugger does).

“The art of debugging is figuring out what you really told your program to do rather than what you thought you told it to do.”” — Andrew Singer

• Reassess: Take a step back. Look at the problem from another perspective. Is there anything that can be abstracted to a more general approach?

“Sometimes we get so lost in the details of a problem that we overlook general principles that would solve the problem at a more general level. […] The classic example of this, of course, is the summation of a long list of consecutive integers, 1 + 2 + 3 + … + n, which a very young Gauss quickly recognized was simply n(n+1)/2, thus avoiding the effort of having to do the addition.” — C. Jordan Ball

Sidenote: Another way of reassessing is starting anew. Delete everything and begin again with fresh eyes. I’m serious. You’ll be dumbfounded at how effective this is.

• Research: Ahh, good ol’ Google. You read that right. No matter what problem you have, someone has probably solved it. Find that person/ solution. In fact, do this even if you solved the problem! (You can learn a lot from other people’s solutions).

Caveat: Don’t look for a solution to the big problem. Only look for solutions to sub-problems. Why? Because unless you struggle (even a little bit), you won’t learn anything. If you don’t learn anything, you wasted your time.

Don’t expect to be great after just one week. If you want to be a good problem-solver, solve a lot of problems!

Practice. Practice. Practice. It’ll only be a matter of time before you recognize that “this problem could easily be solved with .”

How to practice? There are options out the wazoo!

Chess puzzles, math problems, Sudoku, Go, Monopoly, video-games, cryptokitties, bla… bla… bla….

In fact, a common pattern amongst successful people is their habit of practicing “micro problem-solving.” For example, Peter Thiel plays chess, and Elon Musk plays video-games.

“Byron Reeves said ‘If you want to see what business leadership may look like in three to five years, look at what’s happening in online games.’ Fast-forward to today. Elon [Musk], Reid [Hoffman], Mark Zuckerberg and many others say that games have been foundational to their success in building their companies.” — Mary Meeker ( 2017 internet trends report )

Does this mean you should just play video-games? Not at all.

But what are video-games all about? That’s right, problem-solving!

So, what you should do is find an outlet to practice. Something that allows you to solve many micro-problems (ideally, something you enjoy).

For example, I enjoy coding challenges. Every day, I try to solve at least one challenge (usually on Coderbyte ).

Like I said, all problems share similar patterns.

That’s all folks!

Now, you know better what it means to “think like a programmer.”

You also know that problem-solving is an incredible skill to cultivate (the meta-skill).

As if that wasn’t enough, notice how you also know what to do to practice your problem-solving skills!

Phew… Pretty cool right?

Finally, I wish you encounter many problems.

You read that right. At least now you know how to solve them! (also, you’ll learn that with every solution, you improve).

“Just when you think you’ve successfully navigated one obstacle, another emerges. But that’s what keeps life interesting.[…] Life is a process of breaking through these impediments — a series of fortified lines that we must break through. Each time, you’ll learn something. Each time, you’ll develop strength, wisdom, and perspective. Each time, a little more of the competition falls away. Until all that is left is you: the best version of you.” — Ryan Holiday ( The Obstacle is the Way )

Now, go solve some problems!

And best of luck ?

Special thanks to C. Jordan Ball and V. Anton Spraul . All the good advice here came from them.

Thanks for reading! If you enjoyed it, test how many times can you hit in 5 seconds. It’s great cardio for your fingers AND will help other people see the story.

If you read this far, thank the author to show them you care. Say Thanks

Learn to code for free. freeCodeCamp's open source curriculum has helped more than 40,000 people get jobs as developers. Get started

• 1. Micro-Worlds
• 2. Light-Bot in Java
• 3. Jeroos of Santong Island
• 4. Problem Solving and Algorithms
• 5. Creating Jeroo Methods
• 6. Conditionally Executing Actions
• 7. Repeating Actions
• 8. Handling Touch Events
• 9. Adding Text to the Screen

Problem Solving and Algorithms

Learn a basic process for developing a solution to a problem. Nothing in this chapter is unique to using a computer to solve a problem. This process can be used to solve a wide variety of problems, including ones that have nothing to do with computers.

Problems, Solutions, and Tools

I have a problem! I need to thank Aunt Kay for the birthday present she sent me. I could send a thank you note through the mail. I could call her on the telephone. I could send her an email message. I could drive to her house and thank her in person. In fact, there are many ways I could thank her, but that's not the point. The point is that I must decide how I want to solve the problem, and use the appropriate tool to implement (carry out) my plan. The postal service, the telephone, the internet, and my automobile are tools that I can use, but none of these actually solves my problem. In a similar way, a computer does not solve problems, it's just a tool that I can use to implement my plan for solving the problem.

Knowing that Aunt Kay appreciates creative and unusual things, I have decided to hire a singing messenger to deliver my thanks. In this context, the messenger is a tool, but one that needs instructions from me. I have to tell the messenger where Aunt Kay lives, what time I would like the message to be delivered, and what lyrics I want sung. A computer program is similar to my instructions to the messenger.

The story of Aunt Kay uses a familiar context to set the stage for a useful point of view concerning computers and computer programs. The following list summarizes the key aspects of this point of view.

A computer is a tool that can be used to implement a plan for solving a problem.

A computer program is a set of instructions for a computer. These instructions describe the steps that the computer must follow to implement a plan.

An algorithm is a plan for solving a problem.

A person must design an algorithm.

A person must translate an algorithm into a computer program.

This point of view sets the stage for a process that we will use to develop solutions to Jeroo problems. The basic process is important because it can be used to solve a wide variety of problems, including ones where the solution will be written in some other programming language.

An Algorithm Development Process

Every problem solution starts with a plan. That plan is called an algorithm.

There are many ways to write an algorithm. Some are very informal, some are quite formal and mathematical in nature, and some are quite graphical. The instructions for connecting a DVD player to a television are an algorithm. A mathematical formula such as πR 2 is a special case of an algorithm. The form is not particularly important as long as it provides a good way to describe and check the logic of the plan.

The development of an algorithm (a plan) is a key step in solving a problem. Once we have an algorithm, we can translate it into a computer program in some programming language. Our algorithm development process consists of five major steps.

Step 1: Obtain a description of the problem.

Step 2: analyze the problem., step 3: develop a high-level algorithm., step 4: refine the algorithm by adding more detail., step 5: review the algorithm..

This step is much more difficult than it appears. In the following discussion, the word client refers to someone who wants to find a solution to a problem, and the word developer refers to someone who finds a way to solve the problem. The developer must create an algorithm that will solve the client's problem.

The client is responsible for creating a description of the problem, but this is often the weakest part of the process. It's quite common for a problem description to suffer from one or more of the following types of defects: (1) the description relies on unstated assumptions, (2) the description is ambiguous, (3) the description is incomplete, or (4) the description has internal contradictions. These defects are seldom due to carelessness by the client. Instead, they are due to the fact that natural languages (English, French, Korean, etc.) are rather imprecise. Part of the developer's responsibility is to identify defects in the description of a problem, and to work with the client to remedy those defects.

The purpose of this step is to determine both the starting and ending points for solving the problem. This process is analogous to a mathematician determining what is given and what must be proven. A good problem description makes it easier to perform this step.

When determining the starting point, we should start by seeking answers to the following questions:

What data are available?

Where is that data?

What formulas pertain to the problem?

What rules exist for working with the data?

What relationships exist among the data values?

When determining the ending point, we need to describe the characteristics of a solution. In other words, how will we know when we're done? Asking the following questions often helps to determine the ending point.

What new facts will we have?

What items will have changed?

What changes will have been made to those items?

What things will no longer exist?

An algorithm is a plan for solving a problem, but plans come in several levels of detail. It's usually better to start with a high-level algorithm that includes the major part of a solution, but leaves the details until later. We can use an everyday example to demonstrate a high-level algorithm.

Problem: I need a send a birthday card to my brother, Mark.

Analysis: I don't have a card. I prefer to buy a card rather than make one myself.

High-level algorithm:

Go to a store that sells greeting cards Select a card Purchase a card Mail the card

This algorithm is satisfactory for daily use, but it lacks details that would have to be added were a computer to carry out the solution. These details include answers to questions such as the following.

"Which store will I visit?"

"How will I get there: walk, drive, ride my bicycle, take the bus?"

"What kind of card does Mark like: humorous, sentimental, risqué?"

These kinds of details are considered in the next step of our process.

A high-level algorithm shows the major steps that need to be followed to solve a problem. Now we need to add details to these steps, but how much detail should we add? Unfortunately, the answer to this question depends on the situation. We have to consider who (or what) is going to implement the algorithm and how much that person (or thing) already knows how to do. If someone is going to purchase Mark's birthday card on my behalf, my instructions have to be adapted to whether or not that person is familiar with the stores in the community and how well the purchaser known my brother's taste in greeting cards.

When our goal is to develop algorithms that will lead to computer programs, we need to consider the capabilities of the computer and provide enough detail so that someone else could use our algorithm to write a computer program that follows the steps in our algorithm. As with the birthday card problem, we need to adjust the level of detail to match the ability of the programmer. When in doubt, or when you are learning, it is better to have too much detail than to have too little.

Most of our examples will move from a high-level to a detailed algorithm in a single step, but this is not always reasonable. For larger, more complex problems, it is common to go through this process several times, developing intermediate level algorithms as we go. Each time, we add more detail to the previous algorithm, stopping when we see no benefit to further refinement. This technique of gradually working from a high-level to a detailed algorithm is often called stepwise refinement .

The final step is to review the algorithm. What are we looking for? First, we need to work through the algorithm step by step to determine whether or not it will solve the original problem. Once we are satisfied that the algorithm does provide a solution to the problem, we start to look for other things. The following questions are typical of ones that should be asked whenever we review an algorithm. Asking these questions and seeking their answers is a good way to develop skills that can be applied to the next problem.

Does this algorithm solve a very specific problem or does it solve a more general problem ? If it solves a very specific problem, should it be generalized?

For example, an algorithm that computes the area of a circle having radius 5.2 meters (formula π*5.2 2 ) solves a very specific problem, but an algorithm that computes the area of any circle (formula π*R 2 ) solves a more general problem.

Can this algorithm be simplified ?

One formula for computing the perimeter of a rectangle is:

length + width + length + width

A simpler formula would be:

2.0 * ( length + width )

Is this solution similar to the solution to another problem? How are they alike? How are they different?

For example, consider the following two formulae:

Rectangle area = length * width Triangle area = 0.5 * base * height

Similarities: Each computes an area. Each multiplies two measurements.

Differences: Different measurements are used. The triangle formula contains 0.5.

Hypothesis: Perhaps every area formula involves multiplying two measurements.

Example 4.1: Pick and Plant

This section contains an extended example that demonstrates the algorithm development process. To complete the algorithm, we need to know that every Jeroo can hop forward, turn left and right, pick a flower from its current location, and plant a flower at its current location.

Problem Statement (Step 1)

A Jeroo starts at (0, 0) facing East with no flowers in its pouch. There is a flower at location (3, 0). Write a program that directs the Jeroo to pick the flower and plant it at location (3, 2). After planting the flower, the Jeroo should hop one space East and stop. There are no other nets, flowers, or Jeroos on the island.

Analysis of the Problem (Step 2)

The flower is exactly three spaces ahead of the jeroo.

The flower is to be planted exactly two spaces South of its current location.

The Jeroo is to finish facing East one space East of the planted flower.

There are no nets to worry about.

High-level Algorithm (Step 3)

Let's name the Jeroo Bobby. Bobby should do the following:

Get the flower Put the flower Hop East

Detailed Algorithm (Step 4)

Get the flower Hop 3 times Pick the flower Put the flower Turn right Hop 2 times Plant a flower Hop East Turn left Hop once

Review the Algorithm (Step 5)

The high-level algorithm partitioned the problem into three rather easy subproblems. This seems like a good technique.

This algorithm solves a very specific problem because the Jeroo and the flower are in very specific locations.

This algorithm is actually a solution to a slightly more general problem in which the Jeroo starts anywhere, and the flower is 3 spaces directly ahead of the Jeroo.

Java Code for "Pick and Plant"

A good programmer doesn't write a program all at once. Instead, the programmer will write and test the program in a series of builds. Each build adds to the previous one. The high-level algorithm will guide us in this process.

FIRST BUILD

To see this solution in action, create a new Greenfoot4Sofia scenario and use the Edit Palettes Jeroo menu command to make the Jeroo classes visible. Right-click on the Island class and create a new subclass with the name of your choice. This subclass will hold your new code.

The recommended first build contains three things:

The main method (here myProgram() in your island subclass).

Declaration and instantiation of every Jeroo that will be used.

The high-level algorithm in the form of comments.

The instantiation at the beginning of myProgram() places bobby at (0, 0), facing East, with no flowers.

Once the first build is working correctly, we can proceed to the others. In this case, each build will correspond to one step in the high-level algorithm. It may seem like a lot of work to use four builds for such a simple program, but doing so helps establish habits that will become invaluable as the programs become more complex.

SECOND BUILD

This build adds the logic to "get the flower", which in the detailed algorithm (step 4 above) consists of hopping 3 times and then picking the flower. The new code is indicated by comments that wouldn't appear in the original (they are just here to call attention to the additions). The blank lines help show the organization of the logic.

By taking a moment to run the work so far, you can confirm whether or not this step in the planned algorithm works as expected.

THIRD BUILD

This build adds the logic to "put the flower". New code is indicated by the comments that are provided here to mark the additions.

FOURTH BUILD (final)

Example 4.2: replace net with flower.

This section contains a second example that demonstrates the algorithm development process.

There are two Jeroos. One Jeroo starts at (0, 0) facing North with one flower in its pouch. The second starts at (0, 2) facing East with one flower in its pouch. There is a net at location (3, 2). Write a program that directs the first Jeroo to give its flower to the second one. After receiving the flower, the second Jeroo must disable the net, and plant a flower in its place. After planting the flower, the Jeroo must turn and face South. There are no other nets, flowers, or Jeroos on the island.

Jeroo_2 is exactly two spaces behind Jeroo_1.

The only net is exactly three spaces ahead of Jeroo_2.

Each Jeroo has exactly one flower.

Jeroo_2 will have two flowers after receiving one from Jeroo_1. One flower must be used to disable the net. The other flower must be planted at the location of the net, i.e. (3, 2).

Jeroo_1 will finish at (0, 1) facing South.

Jeroo_2 is to finish at (3, 2) facing South.

Each Jeroo will finish with 0 flowers in its pouch. One flower was used to disable the net, and the other was planted.

Let's name the first Jeroo Ann and the second one Andy.

Ann should do the following: Find Andy (but don't collide with him) Give a flower to Andy (he will be straight ahead) After receiving the flower, Andy should do the following: Find the net (but don't hop onto it) Disable the net Plant a flower at the location of the net Face South

Ann should do the following: Find Andy Turn around (either left or right twice) Hop (to location (0, 1)) Give a flower to Andy Give ahead Now Andy should do the following: Find the net Hop twice (to location (2, 2)) Disable the net Toss Plant a flower at the location of the net Hop (to location (3, 2)) Plant a flower Face South Turn right

The high-level algorithm helps manage the details.

This algorithm solves a very specific problem, but the specific locations are not important. The only thing that is important is the starting location of the Jeroos relative to one another and the location of the net relative to the second Jeroo's location and direction.

Java Code for "Replace Net with Flower"

As before, the code should be written incrementally as a series of builds. Four builds will be suitable for this problem. As usual, the first build will contain the main method, the declaration and instantiation of the Jeroo objects, and the high-level algorithm in the form of comments. The second build will have Ann give her flower to Andy. The third build will have Andy locate and disable the net. In the final build, Andy will place the flower and turn East.

This build creates the main method, instantiates the Jeroos, and outlines the high-level algorithm. In this example, the main method would be myProgram() contained within a subclass of Island .

This build adds the logic for Ann to locate Andy and give him a flower.

This build adds the logic for Andy to locate and disable the net.

This build adds the logic for Andy to place a flower at (3, 2) and turn South.

• Python Programming
• C Programming
• Numerical Methods
• Dart Language
• Computer Basics
• Deep Learning
• C Programming Examples
• Python Programming Examples

Problem Analysis

Problem analysis is the process of defining a problem and decomposing overall system into smaller parts to identify possible inputs, processes and outputs associated with the problem. This task is further subdivided into six subtasks namely:

First, we need to know what problem is actually being solved. Making a clear statement of the problem depends upon the size and complexity of the problem. Smaller problems not involving multiple subsystems can easily be stated and then we can move onto the next step of “Program Design”. However, a problem interacting with various subsystems and series of programs require complex analysis, in-depth research and careful coordination of people, procedures and programs.

Before identifying inputs required for the system, we need to identify what comes out of the system. The best way to specify output is to prepare some output forms and required format for displaying result. The best person to judge an output form is the end user of the system i.e. the one who uses the software to his benefit. Various forms can be designed by the programmer which must be examined to see whether they are useful or not.

After having specified the outputs, the input and data required for the system need to be specified as well. One needs to identify the list of inputs required and the source of data. For example, in a simple program to keep student’s record, the inputs could be the student’s name, address, roll-numbers, etc. The sources could be the students themselves or the person supervising them.

When output and inputs are specified, we need to specify process that converts specified inputs into desired output. If the proposed program is to replace or supplement an existing one, a careful evaluation of the present processing procedures needs to be made, noting any improvements that could made. If the proposed system is not designed to replace an existing system, then it is well advised to carefully evaluate another system that addresses a similar problem.

After the successful completion of all the above four steps one needs to see whether the things accomplished so far in the process of problem solving are practical and feasible. To replace an existing system one needs to determine how the potential improvements outperforms existing system or other similar system.

Before concluding the program analysis stage, it is best to record whatever has been done so far in the first phase of program development. The record should contain the statement of program objectives, output and input specifications, processing requirements and feasibility.

UNIT 1: How to Think Like an Engineer

Learning objectives.

• Explain what we mean by “Computational Thinking”.
• Describe the problem being solved in a computational algorithm.
• Explain the process for generating computational algorithms.
• Generate and test algorithms to solve computational problems.
• Evaluate computational algorithms for exactness, correctness, termination, generalizability and understandability.
• Explain the role of programming in the field of Informatics.

Introduction

The goal of this book is to teach you to solve computational problems and to think like an engineer. Computational problems are problems that can be solved by the use of computations (a computation is what you do when you calculate something). Engineers are people who solve problems – they invent, design, analyze, build and test “things” to fulfill objectives and requirements. The single most important skill for you to learn is problem solving. Problem solving means the ability to formulate problems, think creatively about solutions, and express a solution clearly and accurately. As it turns out, the process of learning to program is an excellent opportunity to practice problem-solving skills.

This book strives to prepare you to write well-designed computer programs that solve interesting problems involving data.

Computational Thinking

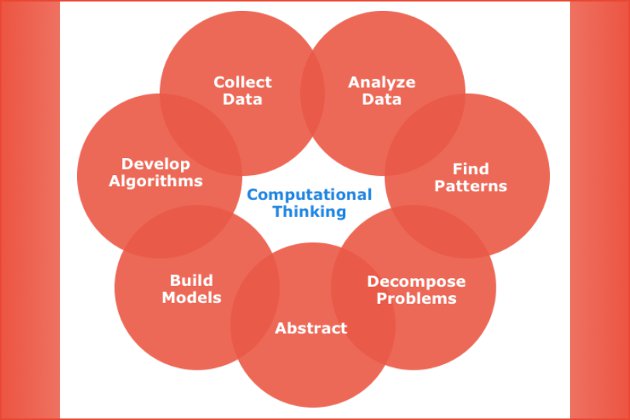
Figure 1: “The seven components to computational thinking”(www.ignitemyfutureinschool.org/about)

Computational Thinking is the thought processes involved in understanding a problem and expressing its solution in a way that a computer can effectively carry out. Computational thinking involves solving problems, designing systems, and understanding human behavior (e.g. what the user needs or wants) – thinking like an engineer. Computational thinking is a fundamental skill for everyone, not just for programmers because computational thinking is what comes before any computing technology. [1]

Computer science is the study of computation — what can be computed and how to compute it whereas computational thinking is:

Conceptualizing , not programming. Computer science is not only computer programming. Thinking like a computer scientist means more than being able to program a computer. It requires thinking at multiple levels of abstraction;

Fundamental , not rote skill. A fundamental skill is something every human being must know to function in modern society. Rote means a mechanical routine;

A way that humans, not computers, think . Computational thinking is a way humans solve problems; it is not trying to get humans to think like computers. Computers are dull and boring; humans are clever and imaginative. We humans make computers exciting. Equipped with computing devices, we use our cleverness to tackle problems we would not dare take on before the age of computing and build systems with functionality limited only by our imaginations;

Complements and combines mathematical and engineering thinking . Computer science inherently draws on mathematical thinking, given that, like all sciences, its formal foundations rest on mathematics. Computer science inherently draws on engineering thinking, given that we build systems that interact with the real world;

Ideas , not artifacts. It’s not just the software and hardware artifacts we produce that will be physically present everywhere and touch our lives all the time, it will be the computational concepts we use to approach and solve problems, manage our daily lives, and communicate and interact with other people;

For everyone, everywhere . Computational thinking will be a reality when it is so integral to human endeavors it disappears as an explicit philosophy. [2]

Figure 2 “Are you happy?” by Typcut http://www.typcut.com/headup/are-you-happy

An algorithm specifies a series of steps that perform a particular computation or task. Throughout this book we’ll examine a number of different algorithms to solve a variety of computational problems.

Algorithms resemble recipes. Recipes tell you how to accomplish a task by performing a number of steps. For example, to bake a cake the steps are: preheat the oven; mix flour, sugar, and eggs thoroughly; pour into a baking pan; set the timer and bake until done.

However, “algorithm” is a technical term with a more specific meaning than “recipe”, and calling something an algorithm means that the following properties are all true:

• An algorithm is an unambiguous description that makes clear what has to be implemented in order to solve the problem. In a recipe, a step such as “Bake until done” is ambiguous because it doesn’t explain what “done” means. A more explicit description such as “Bake until the cheese begins to bubble” is better. In a computational algorithm, a step such as “Choose a large number” is vague: what is large? 1 million, 1 billion, or 100? Does the number have to be different each time, or can the same number be used again?
• An algorithm expects a defined set of inputs. For example, it might require two numbers where both numbers are greater than zero. Or it might require a word, or a list customer names.
• An algorithm produces a defined set of outputs. It might output the larger of the two numbers, an all-uppercase version of a word, or a sorted version of the list of names.
• An algorithm is guaranteed to terminate and produce a result, always stopping after a finite time. If an algorithm could potentially run forever, it wouldn’t be very useful because you might never get an answer.
• Must be general for any input it is given. Algorithms solve general problems (determine if a password is valid); they are of little use if they only solve a specific problem (determine if ‘comp15’ is a valid password)
• It is at the right level of detail…..the person or device executing the instruction know how to accomplish the instruction without any extra information.

Once we know it’s possible to solve a problem with an algorithm, a natural question is whether the algorithm is the best possible one. Can the problem be solved more quickly or efficiently?

The first thing you need to do before designing an algorithm is to understand completely the problem given. Read the problem’s description carefully, then read it again. Try sketching out by hand some examples of how the problem can be solved. Finally consider any special cases and design your algorithm to address them.

An algorithm does not solve a problem rather it gives you a series of steps that, if executed correctly, will result in a solution to a problem.

An Example Algorithm

Let us look at a very simple algorithm called find_max.

Problem : Given a list of positive numbers, return the largest number on the list.

Inputs : A list of positive numbers. This list must contain at least one number. (Asking for the largest number in a list of no numbers is not a meaningful question.)

Outputs : A number, which will be the largest number in the list.

Algorithm :

• Accept a list of positive numbers; set to nums_list
• Set max_number to 0.
• If the number is larger, set max_number to the larger number.
• max_number is now set to the largest number in the list of positive numbers, nums_list.

Does this meet the criteria for being an algorithm?

• Is it unambiguous? Yes. Each step of the algorithm consists of uncomplicated operations, and translating each step into programming code is straight forward.
• Does it have defined inputs and outputs? Yes.
• Is it guaranteed to terminate? Yes. The list nums_list is of finite length, so after looking at every element of the list the algorithm will stop.
• Is it general for any input? Yes. A list of any set of positive numbers works.
• Does it produce the correct result? Yes. When tested, the results are what are expected

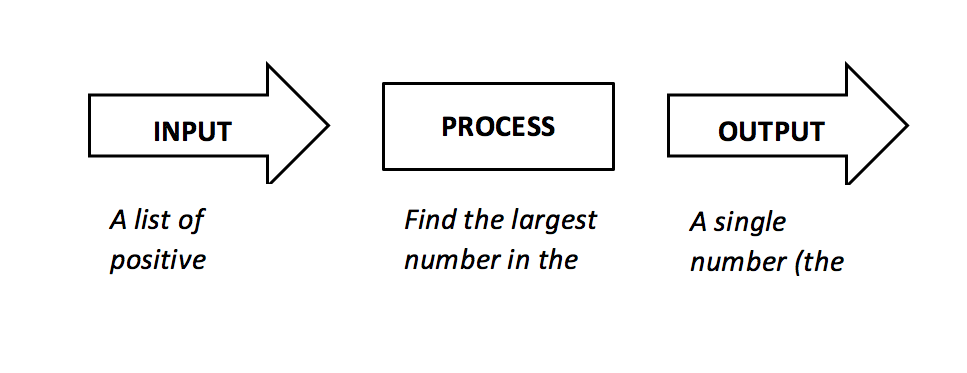
Figure 3: Example Algorithm

How do we know if an algorithm is unambiguous, correct, comes to an end, is general AND is at the right level of detail? We must test the algorithm. Testing means verifying that the algorithm does what we expect it to do. In our ‘bake a cake’ example we know our algorithm is ‘working’ if, in the end, we get something that looks, smells and tastes like a cake.

Verifying your Algorithm

Figure 3 “ Keyboard ” by Geralt is licensed under CC 2

Your first step should be to carefully read through EACH step of the algorithm to check for ambiguity and if there is any information missing. To ensure that the algorithm is correct, terminates and is general for any input we devise ‘test cases’ for the algorithm.

A test case is a set of inputs, conditions, and expected results developed for a particular computational problem to be solved. A test case is really just a question that you ask of the algorithm (e.g. if my list is the three numbers 2, 14, and 11 does the algorithm return the number 14?). The point of executing the test is to make sure the algorithm is correct, that it terminates and is general for any input.

Good (effective) test cases:

• are easy to understand and execute
• are created with the user in mind (what input mistakes will be made? what are the preconditions?)
• make no assumptions (you already know what it is supposed to do)
• consider the boundaries for a specified range of values.

Let us look at the example algorithm from the previous section. The input for the algorithm is ‘a list of positive numbers’. To make it easy to understand and execute keep the test lists short. The preconditions are that the list only contains numbers and these numbers must be positive so include a test with a ‘non-number’ (i.e. a special character or a letter) and a test with a negative number. The boundaries for the list are zero and the highest positive number so include a test with zero and a large positive number. That is it! Here is an example of three different test cases.

Manually, you should step through your algorithm using each of the three test cases, making sure that the algorithm does indeed terminate and that you get your expected result. As our algorithms and programs become more complex, skilled programmers often break each test case into individual steps of the algorithm/program and indicate what the expected result of each step should be. When you write a detailed test case, you don’t necessarily need to specify the expected result for each test step if the result is obvious.

In computer programming we accept a problem to solve and develop an algorithm that can serve as a general solution. Once we have such a solution, we can use our computer to automate the execution. Programming is a skill that allows a competent programmer to take an algorithm and represent it in a notation (a program) that can be followed by a computer. These programs are written in programming languages (such as Python). Writing a correct and valid algorithm to solve a computational problem is key to writing good code. Learn to Think First and coding will come naturally!

The Process of Computational Problem Solving

Computational problem solving does not simply involve the act of computer programming. It is a process, with programming being only one of the steps. Before a program is written, a design for the program must be developed (the algorithm). And before a design can be developed, the problem to be solved must be well understood. Once written, the program must be thoroughly tested. These steps are outlined in Figure 5.

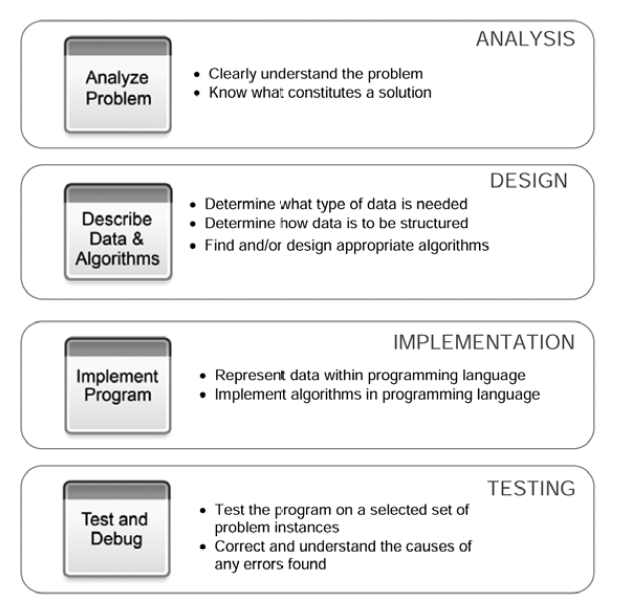
Figure 5: Process of Computational Problem Solving [footnote]Dierbach, Charles. Introduction to Computer Science Using Python: A Computational Problem-solving Focus. Wiley Publishing, 2012, pp17-18.[/footnote]

Values and Variables

A value is one of the basic things computer programs works with, like a password or a number of errors.

Values belong to different types: 21 is an integer (like the number of errors), and ‘comp15’ is a string of characters (like the password). Python lets you give names to values giving us the ability to generalize our algorithms.

One of the most powerful features of a programming language is the ability to use variables. A variable is simply a name that refers to a value as shown below,

Whenever the variable errors appears in a calculation the current value of the variable is used.

We need some way of storing information (i.e. the number of errors or the password) and manipulate them as well. This is where variables come into the picture. Variables are exactly what the name implies – their value can vary, i.e., you can store anything using a variable. Variables are just parts of your computer’s memory where you store some information. Unlike literal constants, you need some method of accessing these variables and hence you give them names.

Programmers generally choose names for their variables that are meaningful and document what the variable is used for. It is a good idea to begin variable names with a lowercase letter . The underscore character (_) can appear in a name and is often used in names with multiple words.

A program is a sequence of instructions that specifies how to perform a computation. The computation might be something mathematical, such as solving a system of mathematical equations or finding the roots of a polynomial, but it can also be a symbolic computation, such as searching and replacing text in a document or something graphical, like processing user input on an ATM device.

What is a Program?

Figure 6: “ Python Code ” by nyuhuhuu is licensed under CC-BY 2.0

The details look different in different computer programming languages, but there are some low-level conceptual patterns (constructs) that we use to write all programs. These constructs are not just for Python programs, they are a part of every programming language.

input Get data from the “outside world”. This might be reading data from a file, or even some kind of sensor like a microphone or GPS. In our initial algorithms and programs, our input will come from the user typing data on the keyboard.

output Display the results of the program on a screen or store them in a file or perhaps write them to a device like a speaker to play music or speak text.

sequential execution Perform statements one after another in the order they are encountered in the script.

conditional execution Checks for certain conditions and then executes or skips a sequence of statements.

repeated execution Perform some set of statements repeatedly, usually with some variation.

reuse Write a set of instructions once and give them a name and then reuse those instructions as needed throughout your program.

Believe it or not, that’s pretty much all there is to it. Every computer application you’ve ever used, no matter how complicated, is made up of constructs that look pretty much like these. So you can think of programming as the process of breaking a large, complex task into smaller and smaller subtasks until the subtasks are simple enough to be performed with one of these basic constructs. The “art” of writing a program is composing and weaving these basic elements together many times over to produce something that is useful to its users.

Computational Problem Design Using the Basic Programming Constructs

The key to better algorithm design and thus to programming lies in limiting the control structure to only three constructs as shown below.

• The Sequence structure (sequential execution)
• The Decision, Selection or Control structure (conditional execution)
• Repetition or Iteration Structure (repeated execution)

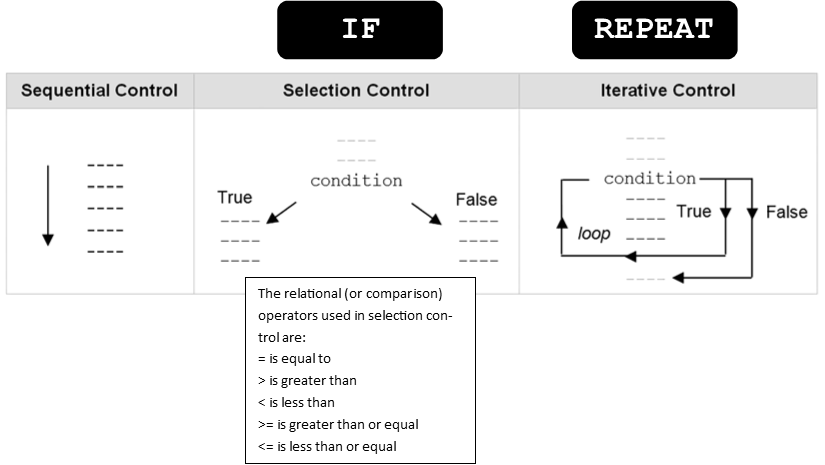
Figure 7: the 3 Programming Constructs

  Let us look at some examples for the sequential control and the selection control.

Sequential Control Example

The following algorithm is an example of sequential control .

Problem : Given two numbers, return the sum and the product of the two numbers.

Inputs : Two numbers.

Outputs : The sum and the product.

• display “Input two numbers”
• sum = number1 + number2
• print “The sum is “, sum
• product = number1 * number2
• print “The product is “, product
• Is it guaranteed to terminate? Yes. Sequential control, by its nature, always ends.
• Is it general for any input? Yes. Any two numbers work in this design.
• Does it produce the correct result? Yes. When tested, the results are what are expected.

Here is an example of three different test cases that are used to verify the algorithm.

Selection Control

The following two algorithms are examples of selection control which uses the ‘IF’ statement in most programming languages.

Problem : Given two numbers, the user chooses to either multiply, add or subtract the two numbers. Return the value of the chosen calculation.

Inputs : Two numbers and calculation option.

Outputs : The value of the chosen calculation.

The relational (or comparison) operators used in selection control are:

= is equal to

> is greater than

< is less than

>= is greater than or equal

<= is less than or equal

<> is not equal to

• display “choose one of the following”
• display “m for multiply”
• display “a for add”
• display “s for subtract”
• accept choice
• display “input two numbers you want to use”
• accept number1, number2
• if choice = m then answer= number1 * number2
• if choice = a then answer= number1 + number2
• if choice = s then answer= number1 -number212. if choice is not m, a, or s then answer is NONE
• display answer
• Is it guaranteed to terminate? Yes. The input is of finite length, so after accepting the user’s choice and the two numbers the algorithm will stop.
• Is it general for any input? Yes. Any two numbers work in this design and only a choice of a’m’, ‘a’, or ‘s’ will result in numeric output.

This example uses an extension of the simple selection control structure we just saw and is referred to as the ‘IF-ELSE’ structure.

Problem : Accept from the user a positive integer value representing a salary amount, return tax due based on the salary amount.

Inputs : One positive integer number.

Outputs : The calculated tax amount.

• accept salary
• If salary < 50000 then
• Tax = 0 Else
• If salary > 50000 AND salary < 100000 then
• Tax = 50000 * 0.05 Else
• Tax = 100000 * 0.30
• display Tax
• Is it guaranteed to terminate? Yes. The input is of finite length, so after accepting the user’s number, even if it is negative, the algorithm will stop.
• Is it general for any input? Yes. Any number entered in this design will work.

Iterative Control Examples

The third programming control is the iterative or, also referred to as, the repetition structure. This control structure causes certain steps to be repeated in a sequence a specified number of times or until a condition is met. This is what is called a ‘loop’ in programming

In all programming languages there are generally two options: an indefinite loop (the Python ‘WHILE’ programming statement) and a definite loop (the Python ‘FOR’ programming statement). We can use these two constructs, WHILE and FOR, for iterations or loops in our algorithms.

Note for Reader: A definite loop is where we know exactly the number of times the loop’s body will be executed. Definite iteration is usually best coded as a Python for loop. An indefinite loop is where we do not know before entering the body of the loop the exact number of iterations the loop will perform. The loop just keeps going until some condition is met. A while statement is used in this case.

The following algorithm is an example of iterative control using WHILE .

Problem : Print each keyboard character the users types in until the user chooses the ‘q’ (for ‘quit’) character.

Inputs : A series of individual characters.

Outputs : Each character typed in by the user.

• initialize (set) letter = ‘a’
• WHILE letter <> ‘q’
• ACCEPT letter
• DISPLAY “The character you typed is”, letter
• Is it guaranteed to terminate? Yes. The input is of finite length, so after accepting the user’s keyboard character, even if it is not a letter, the algorithm will stop.
• Is it general for any input? Yes. Any keyboard character entered in this design will work.

The following algorithm is an example of iterative control using FOR . This statement is used when the number of iterations is known in advance.

Problem : Ask the user how many words they want to enter then print the words entered by the user.

Inputs : Number of words to be entered; this value must be a positive integer greater than zero. Individual words.

Outputs : Each word typed in by the user.

• accept num_words (must be at least one)
• repeat num_words times (FOR 1 to num_words)
• accept word
• DISPLAY “The word you entered is”, word
• Is it guaranteed to terminate? Yes. The input is of finite length, so after accepting the user’s number of words to enter and any characters typed on the keyboard, even if it is not a ‘word’ per say, the algorithm will stop.
• Is it general for any input? Yes. Any positive integer greater than zero and any size ‘word’ will work.

Here is an example of two different test cases that are used to verify the algorithm.

The Role of Programming in the Field of Informatics

Figure8: iPhone apps by Jaap Arriens/NurPhoto via Getty Images (abcnews.go.com)

You see computer programming in use every day. When you use Google or your smartphone, or watch a movie with special effects, there is programing at work. When you order a product over the Internet, there is code in the web site, in the cryptography used to keep your credit card number secure, and in the way that UPS routes their delivery vehicle to get your order to you as quickly as possible.

Programming is indeed important to an informatics professional as they are interested in finding solutions for a wide variety of computational problems involving data.

When you Google the words “pie recipe,” Google reports that it finds approximately 38 million pages, ranked in order of estimated relevance and usefulness. Facebook has approximately 1 billion active users who generate over 3 billion comments and “Likes” each day. GenBank, a national database of DNA sequences used by biologists and medical researchers studying genetic diseases, has over 100 million genetic sequences with over 100 billion DNA base pairs. According to the International Data Corporation, by 2020 the digital universe – the data we create and copy annually – will reach 44 zettabytes, or 44 trillion gigabytes.

Figure 9: The Digital Universe ( www.emc.com/leadership/digital-universe/2014iview/images )

  Doing meaningful things with data is challenging, even if we’re not dealing with millions or billions of things. In this book, we will be working with smaller sets of data. But much of what we’ll do will be applicable to very large amounts of data too.

Unit Summary

Computational Thinking is the thought processes involved in formulating a problem and expressing its solution in a way that a computer—human or machine—can effectively carry out.

Computational Thinking is what comes before any computing technology—thought of by a human, knowing full well the power of automation.

Writing a correct and valid algorithm to solve a computational problem is key to writing good code.

• What are the inputs?
• What are the outputs (or results)?
• Can we break the problem into parts?
• Think about the connections between the input & output.
• Consider designing ‘backwards’.
• Have you seen the problem before? In a slightly different form?
• Can you solve part of the problem?
• Did you use all the inputs?
• Can you test it on a variety of inputs?
• Can you think of how you might write the algorithm differently if you had to start again?
• Does it solve the problem? Does it meet all the requirements? Is the output correct?
• Does it terminate?
• Is it general for all cases?

Practice Problems

• Write about a process in your life (e.g. driving to the mall, walking to class, etc.) and estimate the number of steps necessary to complete the task. Would you consider this a complex or simple task? What happens if you scale that task (e.g. driving two states away to the mall)? Is your method the most efficient? Can you come up with a more efficient way?

• Write an algorithm to find the average of 25 test grades out of a possible 100 points.
• If you are given three sticks, you may or may not be able to arrange them in a triangle. For example, if one of the sticks is 12 inches long and the other two are one inch long, it is clear that you will not be able to get the short sticks to meet in the middle. For any three lengths, there is a simple test to see if it is possible to form a triangle: “If any of the three lengths is greater than the sum of the other two, then you cannot form a triangle. Otherwise, you can.”Write an algorithm that accepts three integers as arguments, and that displays either “Yes” or “No,” depending on whether you can or cannot form a triangle from sticks with the given lengths.
• ROT13 is a weak form of encryption that involves “rotating” each letter in a word by 13 places. To rotate a letter means to shift it through the alphabet, wrapping around to the beginning if necessary, so ‘A’ shifted by 3 is ‘D’ and ‘Z’ shifted by 1 is ‘A’. Write an algorithm that accepts a word and an integer from the user, and that prints a new encrypted word that contains the letters from the original word “rotated” by the given amount (the integer input). For example, “cheer” rotated by 7 is “jolly” and “melon” rotated by −10 is “cubed.”
• Write an algorithm which repeatedly accepts numbers until the user enters “done”. Once “done” is entered, display the total sum of all the numbers, the count of numbers entered, and the average of all the numbers.
• Write an algorithm that sums a series of ten positive integers entered by the user excluding all numbers greater than 100. Display the final sum.
• Wing, Jeannette M. "Computational thinking." Communications of the ACM 49.3 (2006): 33-35. ↵

Privacy Policy

Walkthrough

Programming problem solving walkthrough.

A programming problem solving walkthrough is a written guided description of the journey from a problem to a solution. It aims to teach how to solve programming problems in a methodical and thoughtful manner using the model. In other words, the knowledge to be learned is focused on the "how", and not on the programming language per se.

The walkthrough, as a teaching method, is based on two concepts: worked example from learning sciences and literate programming from computer science.

A worked example is a step-by-step demonstration of how to solve a problem. Learning scientists found out that worked examples are most effective for novices (i.e., the audience of a walkthrough), while performing problem-solving is more beneficial for experts. There are multiple ways of presenting and supporting worked examples , and one of the evidence-based techniques is to include sub-goal labeling, which is about labeling groups of steps in the worked example.

Literate programming by Donald E. Knuth is a programming paradigm in which a program is written as interspersed snippets of executable code and text. The text, which is written in ordinary human language, explains the logic of the code and explains the programmer's thoughts and decisions. Thus a program is perceived much more like an essay.

The walkthrough combines these two powerful ideas for learning the craft of problem solving by programming. It uses the programming problem solving model and its supplements to give a framework for establishing the learning objectives, as well as defining the walkthrough's structure and flow.

The learning objective of a walkthrough is rooted in one of the phases (for example, acquiring the ability to use a specific design strategy). That's in addition to the always-present learning objective of mastering the instrumentation of end-to-end problem solving .

Many times the solving process is hidden, and one gets only the final result, the executable code. Therefore, an essential feature of a walkthrough is making the reasoning explicit, as suggested by literate programming. In other words, it brings the solving process to the surface and documents the train of thought of the problem-solver as they go through each of the phases. In fact, a walkthrough aims to prompt self-explanation by the learners.

A similar but different flavor of a walkthrough is one that is developed by the learners. They choose a programming problem and fill in a provided walkthrough template. The learners improve their ability to solve problems by explicitly documenting their own process.

This page was written with Python in mind, with Jupyter Notebook that serves as the medium for the walkthrough. Notebooks are natural for literate programming , with their capability to mix text, media, and code in cells. Nevertheless, a walkthrough is a teaching method which is beyond one programming language or another, and it can also be developed as a source code file.

Few (opinionated) Principles and Practices

A walkthrough is an active learning activity. It is similar to a tutorial in the sense that it is most effective if the reader follows along by actually performing the tasks being described. In our particular case the tasks are based on the phases of the problem-solving model .

For example:

• Reinterpret the Problem phase - suggest input-output instances.
• Design a Solution phase - write about choosing a data structure, what attributes make it fit.

While it is important to focus on one particular phase so as not to overwhelm the learner, other phases should not be neglected. To keep the student engaged throughout the walkthrough it is suggested to use less demanding, yet active, tasks.

Tasks suggested by phase appear later on this page.

The walkthrough is designed to achieve teachable moments , in which it leads the learners to a point where they discover or apply a concept, an idea or a technique from the learning objectives.

At the same time a walkthrough must manage cognitive load , with a great focus on the external one.

The walkthrough is a "better version of reality" that focuses on the learning, and not on accurate journaling of the problem solving process . By its nature, this process is often messy and non-linear. Meanwhile, the goal of the walkthrough is to guide the learner through solving the problem in a logical and clear manner, without recording all the twists and turns. In that sense, the walkthrough is a "better version of reality", in which the actual steps are filtered and distilled to support the designer's learning objectives efficiently.

The text and code should be written in expository style . Even if a program has a hierarchical (tree) design, it this might not mean that this structure is the best for its development.

A problem should be solved and explored in a psychologically correct order , following the solver's "stream of consciousness" . The objective is to go through the process of solving, and a walkthrough inherently performs a "linearization" of this path. As Donald E. Knuth wrote:

My experiences have led me to believe that a person reading a program is likewise, ready to comprehend it by learning its various parts in approximately the order in which it was written.

The walkthrough is intended to be perceived as a dialogue with the learner . Of course, this is impossible due to the non-interactive format, but aimed as aspiration.

Walkthroughs are not stand alone but should be considered in context of a unit or a course. After the learners worked on the walkthrough, a wrap-up session (that might include a presentation or live coding of partial or complete solution) should take place.

Use of real-word problems or cover story can increase the motivation of the learners.

It is advised to limit the external permitted materials for the learners.

Checklist / Rubric

This is an opinionated checklist of all the points that a decent walkthrough should fulfill. It refers to the complete walkthrough after a learner performs all the tasks. It is up to the developer to decide which parts are already presented at the beginning and which are left to the learners.

• Get something working and keep it working:
• First writing code in cells, testing it and only then encapsulating into functions

Reinterpret the Problem

• Rephrasing the problem statement in their own words
• Writing the solution contract
• Meaning and (Python) type
• One or few input-output pairs of concrete instances (it doesn't need to be comprehensive right now, it is not the Test phase)

Design a Solution

• Ultimately, a walkthrough should break down the problem into hierarchical sub-problems; in other words, it should present an outline of the solution decomposed into sub-problems.
• Following the DRY (Don't Repeat Yourself ) design principle - Identifying repeating sub-problems
• A mapping between the information in the problem/solution domain to a data-structure (either primitive or composed, flat or nested) in Python
• Describing the meaning of the data structure, the relationship between its components and the required operation (a.k.a questions)
• Transforming well the design into code
• Pythonic Code - Python Idioms
• Meaningful Names
• Using Comments
• Using Helper Functions when needed (e.g., for following DRY)
• Black box (e.g., trivial cases, simplest non-trivial cases, edge cases, corner cases - but it is not mandatory to write the type)
• White box - coverage / path-complete
• Scenario - Using the language of the problem phase/domain
• Instance - Concrete Input-Output pairs
• The test case follows the simplicity principle - the instance(s) should be the simplest possible to test the scenario.
• Following the empirical approach for debugging (reproduce, diagnose, fix, repeat, reflect)
• Diagnose - Focus on reasoning on the available clues (e.g., the bug itself - input/output and trace-back, reading the code with a critical eye, using the print function)

Evaluate & Reflect

• Functionality
• Design & Code
• Readability, Style & Documentation
• Alignment between the presented problem solving process and the takeaways
• Postmortem of the problem solving or debugging process
• Self-debugging - what the programmer can learn from solving this problem.

Solution Program - Solving the Problem

• Copy-paste and organize all the necessary code for a complete solution of the problem in one cell or py file, and execute it to solve the original problem. Note that it might require asking the learners to combine code snippets from different parts of the notebook.
• The code in the solution section is self-contained for execution, and doesn't depend on other snippets of code from the previous steps.
• This section also contains tests of the solution code.

Tips for Developing a Walkthrough

The Carpentries Curriculum Development Handbook is an excellent resource for how to develop a curriculum in computing and what it says is equally applicable to developing a walkthrough.

First of all, set the learning objectives using the programming problem solving model terminology.

Form a problem - choose an algorithmic one or real-world one.

Solve the problem, document your process based on the model, pay attention to your mistakes and bugs.

Reflect on your problem solving process and try to distill it into steps and teachable moments.

Refactor your code and remove clutter. While it doesn't have to be the best possible, make sure to adjust for the required ability of your learners.

Write an outline of the walkthrough and embed your code in the relevant sections. Validate it with a checklist .

Decide what tasks the learners should do, making sure they align with the learning objectives.

Write the complete text of the walkthrough that guides the learners. It is advised to use the plural first person pronoun "we".

Run a pilot of the walkthrough on a small group of learners.

Repeat and improve!

Suggested Tasks by Phase

• Phrase the problem in your own words
• Write three examples of input-output pairs for the problem
• Write the solution of the problem or of a function (in the docstring)
• Write a design (either as text or as a diagram) for a problem or a sub-problem
• Choose a data structure and reason about it
• Describe how to solve the problem "by hand" for one specific input
• Solve a Parson's Puzzle (or the two-dimensional flavor ). It can be created and embedded in Jupyter Notebook with http://parsons.problemsolving.io
• Write code according to a design (either done by the learner or given in the walkthrough)
• Draw an environment diagram
• Answer questions about it
• Write a docstring to a function
• Give meaningful names for variables in the code
• Extract its design (e.g., write a "design tweet" with a maximum of 240 characters)
• Discuss its design - why did the solver choose that particular design and not another, especially pay attention to the data structures
• Write test cases for the problem or function
• Fix a bug in a given piece of code
• Describe a bug you had while solving the problem, and explain how you fixed it
• Evaluate a given piece of code
• Evaluate your code
• Reflect on your problem solving process

Repeat & Improve

• Refactor a given piece of code (e.g., because of speed or design issues)

Additional ideas and inspiration for tasks can be found in the Exercise types chapter from "Teaching Tech Together" and in the Catalog of pedagogical patterns chapter from "Teaching and Learning with Jupyter".

• A Walkthrough is a written guided description of the journey from a problem to a solution.
• It aims to teach how to solve programming problems in a methodical and thoughtful manner using the model.
• The conceptual roots of the walkthrough as a teaching method are the ideas of worked examples and literate programming .
• It is designed to prompt self-explanation by the learners.
• Jupyter Notebook serves as the medium, and it includes active learning tasks.
• Walkthroughs - Open Education Resources
• Worked and faded examples - MIT Open Learning
• Skudder, B., & Luxton-Reilly, A. (2014, January). Worked examples in computer science . In Proceedings of the Sixteenth Australasian Computing Education Conference-Volume 148 (pp. 59-64). Australian Computer Society, Inc..
• Lauren Margulieux - Research and Papers - Subgoal Labels and Worked Examples
• Literate Programming website
• Knuth, D. E. (1984). Literate programming . The Computer Journal, 27(2), 97-111.
• Exercise Types - Teaching Tech Together
• Catalog of Pedagogical Patterns - Teaching and Learning with Jupyter
• The Carpentries Curriculum Development Handbook

Copyright © 2020 Shlomi Hod. All rights reserved.

results matching " "

No results matching " ".

• Analysis of Algorithms
• Backtracking
• Dynamic Programming
• Divide and Conquer
• Geometric Algorithms
• Mathematical Algorithms
• Pattern Searching
• Bitwise Algorithms
• Branch & Bound
• Randomized Algorithms

The Role of Algorithms in Computing

Algorithms play a crucial role in computing by providing a set of instructions for a computer to perform a specific task. They are used to solve problems and carry out tasks in computer systems, such as sorting data , searching for information , image processing , and much more. An algorithm defines the steps necessary to produce the desired outcome , and the computer follows the instructions to complete the task efficiently and accurately. The development of efficient algorithms is a central area of computer science and has significant impacts in various fields, from cryptography and finance to machine learning and robotics.

Algorithms are widely used in various industrial areas to improve efficiency, accuracy, and decision-making. Some of the key applications include:

1.Manufacturing: Algorithms are used to optimize production processes and supply chain management, reducing waste and increasing efficiency.

2.Finance: Algorithms are used to analyze financial data and make predictions, enabling traders and investors to make informed decisions.

3.Healthcare: Algorithms are used to process and analyze medical images, assist in diagnosing diseases, and optimize treatment plans.4Retail: Algorithms are used for customer relationship management, personalized product recommendations, and pricing optimization.

4.Transportation: Algorithms are used to optimize routes for delivery and transportation, reducing fuel consumption and increasing delivery speed.

5.Energy: Algorithms are used to optimize energy generation, distribution, and consumption, reducing waste and increasing efficiency.

6.Security: Algorithms are used to detect and prevent security threats, such as hacking, fraud, and cyber-attacks.

In these and many other industries, algorithms play a crucial role in automating tasks, improving decision-making, and enhancing overall performance and efficiency.

Algorithms are fundamental to computing and play a crucial role in many aspects of the field. Some of the key needs and applications of algorithms in computing include:

1.Data processing: Algorithms are used to process and analyze large amounts of data, such as sorting and searching algorithms.

2.Problem solving: Algorithms are used to solve computational problems, such as mathematical problems, optimization problems, and decision-making problems.

3.Computer graphics: Algorithms are used to create and process images and graphics, such as image compression algorithms and computer-generated graphics algorithms.

4.Artificial Intelligence: Algorithms are used to develop intelligent systems, such as machine learning algorithms, natural language processing algorithms, and computer vision algorithms.

5.Database management: Algorithms are used to manage and organize large amounts of data in databases, such as indexing algorithms and query optimization algorithms.

6.Network communication: Algorithms are used for efficient communication and data transfer in networks, such as routing algorithms and error correction algorithms.

7.Operating systems: Algorithms are used in operating systems for tasks such as process scheduling, memory management, and disk management.

In computing, algorithms are essential for solving complex problems and tasks, improving efficiency and performance, and enabling new technologies and applications.

Algorithms play a critical role in networking and communication systems, enabling efficient and reliable data transfer and communication. Some of the key applications of algorithms in networking include:

1.Routing: Algorithms are used to determine the best path for data to travel from one device to another, such as shortest path algorithms and load balancing algorithms.

2.Error correction: Algorithms are used to detect and correct errors that occur during data transmission, such as cyclic redundancy check (CRC) algorithms and forward error correction (FEC) algorithms.

3.Data compression: Algorithms are used to reduce the amount of data being transmitted, such as Huffman coding and run-length encoding algorithms.

4.Network security: Algorithms are used to secure networks and protect against attacks, such as encryption algorithms and authentication algorithms.

5.Quality of Service (QoS): Algorithms are used to prioritize different types of data and ensure that critical applications receive adequate bandwidth, such as traffic shaping algorithms and congestion control algorithms.

6.Wireless networks: Algorithms are used in wireless networks for tasks such as signal optimization, channel allocation, and power control.

7.Network topology: Algorithms are used to analyze and optimize network topology, such as graph algorithms and network partitioning algorithms.

In networking, algorithms play a vital role in ensuring efficient and reliable data transfer, maintaining network security, and optimizing network performance.

Pre-requisite: Introduction to Algorithms

• The word Algorithm means “a process or set of rules to be followed in calculations or other problem-solving operations”. Therefore Algorithm refers to a set of rules/instructions that step-by-step define how a work is to be executed upon in order to get the expected results.
• Algorithms are at the core of most techniques used in contemporary computers alongside other technologies.
• An algorithm is an abstraction of a program to be executed on a physical machine(model of Computation).

Algorithm Design Technique  

• Strategy or paradigm          — General approach to solve program algorithmically 
• Brute Force           — Straight forward technique with naïve approach 
• Divide and conquer — problem is divided into smaller instances
• Decrease and conquer — Instance size is decreased to solve the problem 
• Transform and conquer — Instance is modified and then solved 
• Dynamic Programming — Results of smaller , reoccurring  instances are obtained to solve problem
• Greedy Technique — Solve the problem by making locally optimal decisions 

Analysis of Algorithm

• Time Efficiency — Indicates how fasts algorithm runs
• Space Efficiency — How much extra memory the algorithm needs to complete its execution
• Simplicity — Generating sequence of instructions which are easy to understand 
• Generality — Range of inputs it can accept .  

Practical applications of algorithms:

• The Internet without which it is difficult to imagine a day is the result of clever and efficient algorithms . With the aid of these algorithms, various sites on the Internet are able to manage and manipulate this large volume of data. Finding good routes on which the data will travel and using search engine to find pages on which particular information is present.
• Another great milestone is the Human Genome Project which has great progress towards the goal of identification of the 100000 genes in human DNA, determining the sequences of the 3 billion chemical base pairs that make up the human DNA, storing this huge amount of information in databases, and developing tools for data analysis. Each of these steps required sophisticated and efficient algorithms.
• The day-to-day electronic commerce activities is hugely dependent on our personal information such as credit/debit card numbers, passwords, bank statements, OTPs and so on. The core technologies used include public-key cryptography and digital signatures which are based on numerical algorithms and number theory .
• In manufacturing and other commercial enterprises where resources need to be allocated scarcely in the most beneficial way.
• Or a institution may want to determine where to spend money buying advertising in order to maximize the chances of their institution to grow.
• In a transportation firm such as a trucking or railroad company, may have financial interest in finding shortest path through a road or rail network because taking shortest path result in lower labour or fuel costs.
• Or a routing node on the Internet may need to find the shortest path through the network in order to route a message quickly.
• Even an application that does not require algorithm content at the application level relies heavily on algorithms as the application depends on hardware, GUI, networking or object orientation and all of these make an extensive use of algorithms.

The role of algorithms in computing is crucial as they are the backbone of any software application or system. Here are some advantages, disadvantages, important points, and reference books related to the role of algorithms in computing:

Advantages:

• Algorithms provide a systematic approach to solving problems and performing tasks efficiently.
• Algorithms can be optimized to improve the performance of software applications and systems.
• Algorithms can be reused in different applications and systems, which can save time and resources.

Disadvantages:

• Poorly designed algorithms can cause software applications and systems to perform poorly or fail altogether.
• The design and optimization of algorithms can be time-consuming and require a high level of expertise.
• Algorithms may not always be suitable for certain types of problems or tasks.

Important points:

• Algorithms are a set of steps or instructions that define a process or method for solving a problem or performing a task.
• The efficiency of an algorithm is measured by its time and space complexity.
• Different algorithms may be better suited for different types of problems or tasks.
• The design and optimization of algorithms are ongoing processes that require constant attention and improvement.

Reference books:

• “Introduction to Algorithms” by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein is a comprehensive guide to algorithm design and analysis.
• “The Art of Computer Programming” by Donald Knuth is a classic text on algorithms and programming, which provides a thorough overview of the role of algorithms in computing.
• “Algorithms” by Robert Sedgewick and Kevin Wayne is a modern and practical guide to algorithm design and analysis.
• “Algorithm Design” by Jon Kleinberg and Éva Tardos provides a modern approach to algorithm design, with a focus on real-world applications.

Similar Reads

Please login to comment..., improve your coding skills with practice.

What kind of Experience do you want to share?

Problem Solving Through Programming in C

In this lesson, we are going to learn Problem Solving Through Programming in C. This is the first lesson while we start learning the C language.

So let’s start learning the C language.

Table of Contents

Introduction to Problem Solving Through Programming in C

Regardless of the area of the study, computer science is all about solving problems with computers. The problem that we want to solve can come from any real-world problem or perhaps even from the abstract world. We need to have a standard systematic approach to problem solving through programming in c.

computer programmers are problem solvers. In order to solve a problem on a computer, we must know how to represent the information describing the problem and determine the steps to transform the information from one representation into another.

In this chapter, we will learn problem-solving and steps in problem-solving, basic tools for designing solution as an algorithm, flowchart , pseudo code etc.

A computer is a very powerful and versatile machine capable of performing a multitude of different tasks, yet it has no intelligence or thinking power.

The Computer performs many tasks exactly in the same manner as it is told to do. This places responsibility on the user to instruct the computer in a correct and precise manner so that the machine is able to perform the required job in a proper way. A wrong or ambiguous instruction may sometimes prove dangerous.

The computer cannot solve the problem on its own, one has to provide step by step solutions of the problem to the computer. In fact, the task of problem-solving is not that of the computer.

It is the programmer who has to write down the solution to the problem in terms of simple operations which the computer can understand and execute.

Problem-solving is a sequential process of analyzing information related to a given situation and generating appropriate response options.

In order to solve a problem with the computer, one has to pass through certain stages or steps. They are as follows:

Steps to Solve a Problem With the Computer

Step 1: understanding the problem:.

Here we try to understand the problem to be solved in totally. Before with the next stage or step, we should be absolutely sure about the objectives of the given problem.

Step 2: Analyzing the Problem:

After understanding thoroughly the problem to be solved, we look at different ways of solving the problem and evaluate each of these methods.

The idea here is to search for an appropriate solution to the problem under consideration. The end result of this stage is a broad overview of the sequence of operations that are to be carried out to solve the given problem.

Step 3: Developing the solution:

Here, the overview of the sequence of operations that was the result of the analysis stage is expanded to form a detailed step by step solution to the problem under consideration.

Step 4: Coding and Implementation:

The last stage of problem-solving is the conversion of the detailed sequence of operations into a language that the computer can understand. Here, each step is converted to its equivalent instruction or instructions in the computer language that has been chosen for the implantation.

The vehicle for the computer solution to a problem is a set of explicit and unambiguous instructions expressed in a programming language. This set of instruction is called a program with problem solving through programming in C .

A program may also be thought of as an algorithm expressed in a programming language. an algorithm, therefore, corresponds to a solution to a problem that is independent of any programming language .

To obtain the computer solution to a problem once we have the program we usually have to supply the program with input or data. The program then takes this input and manipulates it according to its instructions. Eventually produces an output which represents the computer solution to the problem.

The problem solving is a skill and there are no universal approaches one can take to solving problems. Basically one must explore possible avenues to a solution one by one until she/he comes across the right path to a solution.

In general, as one gains experience in solving problems, one develops one’s own techniques and strategies, though they are often intangible. Problem-solving skills are recognized as an integral component of computer programming.

Note: Practice C Programs for problem solving through programming in C.

Problem Solving Steps

Problem-solving is a creative process which defines systematization and mechanization. There are a number of steps that can be taken to raise the level of one’s performance in problem-solving.

A problem-solving technique follows certain steps in finding the solution to a problem. Let us look into the steps one by one:

1. Problem Definition Phase:

The success in solving any problem is possible only after the problem has been fully understood. That is, we cannot hope to solve a problem, which we do not understand. So, the problem understanding is the first step towards the solution of the problem.

In the problem definition phase, we must emphasize what must be done rather than how is it to be done. That is, we try to extract the precisely defined set of tasks from the problem statement.

Inexperienced problem solvers too often gallop ahead with the task of the problem – solving only to find that they are either solving the wrong problem or solving the wrong problem or solving just one particular problem.

2. Getting Started on a Problem:

There are many ways of solving a problem and there may be several solutions. So, it is difficult to recognize immediately which path could be more productive. Problem solving through programming in C.

Sometimes you do not have any idea where to begin solving a problem, even if the problem has been defined. Such block sometimes occurs because you are overly concerned with the details of the implementation even before you have completely understood or worked out a solution.

The best advice is not to get concerned with the details. Those can come later when the intricacies of the problem have been understood.

3. Use of Specific Examples:

To get started on a problem, we can make use of heuristics i.e the rule of thumb. This approach will allow us to start on the problem by picking a specific problem we wish to solve and try to work out the mechanism that will allow solving this particular problem.

It is usually much easier to work out the details of a solution to a specific problem because the relationship between the mechanism and the problem is more clearly defined.

This approach of focusing on a particular problem can give us the foothold we need for making a start on the solution to the general problem.

4. Similarities Among Problems:

One way to make a start is by considering a specific example. Another approach is to bring the experience to bear on the current problems. So, it is important to see if there are any similarities between the current problem and the past problems which we have solved.

The more experience one has the more tools and techniques one can bring to bear in tackling the given problem. But sometimes, it blocks us from discovering a desirable or better solution to the problem.

A skill that is important to try to develop in problem-solving is the ability to view a problem from a variety of angles.

One must be able to metaphorically turn a problem upside down, inside out, sideways, backwards, forwards and so on. Once one has developed this skill it should be possible to get started on any problem.

5. Working Backwards from the Solution:

In some cases, we can assume that we already have the solution to the problem and then try to work backwards to the starting point. Even a guess at the solution to the problem may be enough to give us a foothold to start on the problem.

We can systematize the investigations and avoid duplicate efforts by writing down the various steps taken and explorations made.

Another practice that helps to develop the problem-solving skills, once we have solved a problem, to consciously reflect back on the way we went about discovering the solution.

General Problem Solving Strategies:

There are a number of general and powerful computational strategies that are repeatedly used in various guises in computer science.

Often it is possible to phrase a problem in terms of one of these strategies and achieve considerable gains in computational efficiency.

1. Divide and Conquer:

The most widely known and used strategy, where the basic idea is to break down the original problem into two or more sub-problems, which is presumably easier or more efficient to solve.

The Splitting can be carried on further so that eventually we have many sub-problems, so small that further splitting is no necessary to solve them. We shall see many examples of this strategy and discuss the gain in efficiency due to its application.

2. Binary Doubling:

This is the reverse of the divide and conquers strategy i.e build-up the solution for a larger problem from solutions and smaller sub-problems.

3. Dynamic Programming:

Another general strategy for problem-solving which is useful when we can build-up the solution as a sequence of the intermediate steps. Problem Solving through programming in C.

The travelling salesman problem falls into this category. The idea here is that a good or optimal solution to a problem can be built-up from good or optimal solutions of the sub-problems.

4. General Search, Back Tracking and Branch-and-Bound:

All of these are variants of the basic dynamic programming strategy but are equally important.

Share This Story, Choose Your Platform!

Related posts.

What is Preprocessor in C

What is File Handling in C

Structures and Unions in C