single stage transistor amplifier experiment

Electronics Post

Single stage transistor amplifier.

When in an amplifier circuit only one transistor is used for amplifying a weak signal, the circuit is known as single stage amplifier.

However, a practical amplifier consists of a number of single stage amplifiers and hence  a complex circuit. Therefore, such a complex circuit can be conveniently split into several single stages and can be effectively analysed.

The above fig. shows a single stage transistor amplifier.

When a weak a.c. signal is applied to the base of the transistor, a small base current starts flowing in the input circuit.

Due to transistor action, a much larger (β times the base current) a.c. current flows through the the load Rc in the output circuit.

Since the value of load resistance Rc is very high, a large voltage will drop across it.

Thus, a weak signal applied in the base circuit appears in amplified form in the collector circuit. In this way the transistor acts as an amplifier.

Practical Circuit of Transistor Amplifier

To achieve faithful amplification in a transistor amplifier, we must use proper associated circuitry with the transistor.

A practical single stage transistor amplifier circuit is shown in fig. below.

The various circuit elements and their functions are described as follows :

(i) Biasing Circuit

The resistances R 1 , R 2   and R E  provide biasing and stabilisation.

The biasing circuit must establish a proper operating point otherwise a part of the negative half cycle of the signal may be cut off in the output and you will get faithful amplification.

(ii) Input Capacitor (C in )

An electrolytic capacitor of value 10 μF is used to couple the signal to the base of the transistor.

Otherwise, the signal source resistance will come across R 2  and thus can change the bias.

This capacitor allows only the a.c. signal to flow but isolates the signal source from R 2 .

(iii) Emitter Bypass Capacitor (C E )

An emitter bypass capacitor of value 100 μF is used in parallel with R E  to provide a low reactance path to the amplified a.c. signal.

If this capacitor is not connected in the output circuit then the amplified a.c. signal will flow through R E  and cause a voltage drop across it, thereby reducing the output voltage.

(iv) Coupling Capacitor (C C )

The coupling capacitor of value 10 μF is used to couple one stage of amplification to the next stage.

If it is not used, the bias condition of the next stage will be drastically changed due to the shunting effect of R C  . This is because R C  will come in parallel with the resistance R 1  of the biasing circuit of the next stage amplifier circuit and hence, alter the biasing condition of the next stage.

Therefore, the coupling capacitor is used to isolates the d.c. of one stage from the next stage and allows the a.c. signal only.

Various Circuit Currents

(i) base current.

When no signal is applied in the base circuit, d.c. base current I B, also known as zero signal base current flows due to the biasing circuit.

When a.c. signal is applied, a.c. base current i b  flows in the base circuit.

Hence, the total base current i B  is given by :

(ii) Collector Current

When no signal is applied, a d.c. collector current I C, also known as zero signal collector current flows due to the biasing circuit.

When a.c. signal is applied, a.c. collector current i c also flows in the collector circuit.

Hence, the total collector current i C  is given by :

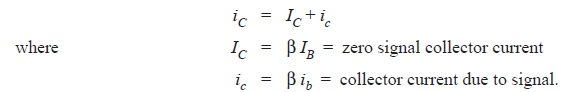
(iii) Emitter Current

When no signal is applied, a d.c. emitter current I E,  flows due to the biasing circuit.

When a.c. signal is applied, a.c. emitter current i e  also flows .

Hence, the total emitter current i E  is given by :

It is useful to keep in mind that :

Now base current is usually very small, therefore, we can take the approximation :

D.C. and A.C. Equivalent Circuits

To analyse the action of a transistor in a simple way, the analysis is divided into two parts such as; d.c. analysis and a.c. analysis.

In d.c. analysis, we will consider all the d.c. sources at the same time and work out the d.c. currents voltages in the circuit.

Similarly, in a.c. analysis, we will consider all the a.c. sources at the same time and work out the a.c. currents and voltages .

For this analysis let us consider the amplifier circuit shown in fig. below .

(1)  D.C. Equivalent Circuit

In the d.c. equivalent circuit of a transistor amplifier, only d.c. conditions must be considered.

So let us assume there is no signal applied to the circuit.

Since, d.c. currents can not pass through the capacitors, hence, all the capacitors look like open circuits in the d.c. equivalent circuit.

Therefore, to draw the d.c. equivalent circuit, the following two steps are applied to the transistor amplifier circuit :

• Make all the a.c. sources zero/Remove all the a.c sources
• Open all the capacitors

Applying these two steps to the circuit shown in fig.3, we will get the d.c. equivalent circuit as shown in fig. below.

Now we can easily calculate the d.c. currents and voltages from this circuit.

(2) A.C. Equivalent Circuit

In the a.c. equivalent circuit of a transistor amplifier, only a.c. conditions must be considered.

In this case, d.c. voltage is not so important hence, may be assumed to be zero.

The capacitors are used in the circuit to couple or bypass the a.c. signal.

The capacitors are generally taken of large values so as to appear as short circuits to the a.c. signal.

Therefore, to draw the a.c. equivalent circuit, the following two steps are applied to the transistor amplifier circuit :

• Make all the d.c. sources  zero/Remove all the d.c. sources
• Short all the capacitors

Applying these two steps to the circuit shown in fig.3, we will get the a.c. equivalent circuit as shown in fig. below.

Now we can easily calculate the a.c. currents and voltages from this circuit.

Voltage Gain of Single stage Transistor Amplifier

The voltage gain of a single stage transistor amplifier is the ratio of a.c. output voltage to a.c. input signal voltage.

Hence, in order to determine the voltage gain, you should consider only the a.c. currents and voltages in the circuit. In other words you have to consider the a.c. equivalent circuit of the transistor amplifier.

The a.c. equivalent circuit of a transistor amplifier is shown in fig. below.

As far as a.c. signal is concerned, load  R C  appears in parallel with R L .

Therefore, the effective load resistance for a.c. is given by :

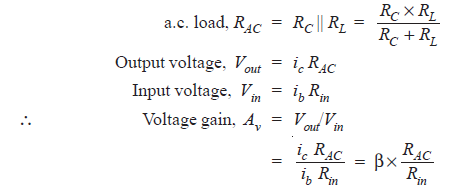
Incidentally, power gain is given by :

Hi! I am Sasmita . At ElectronicsPost.com I pursue my love for teaching. I am an M.Tech in Electronics & Telecommunication Engineering. And, if you really want to know more about me, please visit my "About" Page. Read More

• Evaluation Boards & Kits
• FPGA Reference Designs
• Quick Start Guides
• Linux Software Drivers
• Microcontroller Software Drivers
• ACE Software
• Technical Guides
• University Program Overview
• ADALM1000 (M1k) Active Learning Module
• ADALM2000 (M2k) Active Learning Module
• ADALP2000 Parts kit for Circuits
• ADALM-PLUTO SDR Active Learning Module
• Teaching and Lab Materials
• Wiki Site Map
• Recent Changes
• Media Manager
• Analog Devices Wiki

Table of Contents

9.1 basic amplifiers, 9.2.1 dc bias techniques, common emitter/source, 9.2.2 small signal voltage gain, common emitter or source, 9.2.3 small signal input impedance, common emitter or source, 9.2.4 small signal output impedance, common emitter or source, 9.2.5 common emitter and source lab activities, 9.3.1 dc biasing techniques, current follower or common base/gate amplifier, 9.3.2 small signal voltage gain, current follower or common base/gate amplifier, 9.3.3 input impedance, current follower or common base/gate amplifier, 9.3.4 output impedance, current follower or common base/gate amplifier, 9.4 voltage followers (also called emitter or source follower or common collector or drain amplifiers), 9.4.1 dc biasing techniques, voltage follower or common collector/drain amplifier, 9.4.2 voltage gain, common collector or drain amplifier, example 9.4.2 calculating the voltage gain, 9.4.3 input impedance, voltage follower (common collector or drain), 9.4.4 output impedance, voltage follower (common collector or drain), 9.4.5 voltage follower (common collector or drain) lab activities, 9.5.1 small signal voltage gain with emitter/source degeneration, 9.5.2 small signal input impedance with emitter/source degeneration, 9.5.3 small signal output impedance with emitter/source degeneration, 9.5.4 dc biasing techniques with emitter/source degeneration, 9.5.5 summary - performing small-signal analyses:, 9.6 miller’s theorem, 9.7.1 mos version, 9.7.2 bjt version dc biasing techniques, example 9.7.2 using miller’s theorem, exercise 9.7, 9.7.5 the miller effect, example 9.7.3 miller capacitance example, appendix: source absorption theorem, example a1: finding the emitter resistance using source absorption theorem, at1 diode bias generation, chapter 9: single transistor amplifier stages:.

The term amplifier as used in this chapter means a circuit (or stage) using a single active device rather than a complete system such as an integrated circuit operational amplifier. An amplifier is a device for increasing the power of a signal. This is accomplished by taking energy from a power supply and controlling the output to duplicate the shape of the input signal but with a larger (voltage or current) amplitude. In this sense, an amplifier may be thought of as modulating the voltage or current of the power supply to produce its output.

The basic amplifier, figure 9.1, has two ports and is characterized by its gain, input impedance and output impedance. An ideal amplifier has infinite input impedance (R in = ∞), zero output impedance (R out = 0) and infinite gain (A vo = ∞) and infinite bandwidth if desired.

Figure 9.1 Basic Amplifier Model

The transistor, as we have seen in the previous chapter, is a three-terminal device. Representing the basic amplifier as a two port network as in figure 9.1, there would need to be two input and two output terminals for a total of four. This means one of the transistor terminals must be common to both the input and output circuits. This leads to the names common emitter, etc. for the three basic types of amplifiers. The easiest way to determine if a device is connected as common emitter/source, common collector/drain, or common base/gate is to examine where the input signal enters and the output signal leaves. The remaining terminal is what is thus common to both input and output. In this chapter we will primarily be using n-type transistors (NPN, NMOS) in the example circuits. The same basic amplifier stages can just as easily be implemented using p-type transistors (PNP, PMOS). When larger multi-stage amplifiers are assembled, both types of transistors are often interspersed with each other.

Building-block amplifier stages:

• Inverting voltage amplifier (also called Common emitter or Common source amplifier)
• Current Follower (also called Common base or Common gate or cascode)
• Voltage Follower (also called Common collector or Common drain amplifier)
• Series feedback (more commonly: emitter/source degeneration)
• Shunt feedback

9.2 The inverting voltage amplifier or Common emitter/source

The common emitter/source amplifier is one of three basic single-stage amplifier topologies. The BJT and MOS versions function as an inverting voltage amplifier and are shown in figure 9.2. The base or gate terminal of the transistor serves as the input, the collector or drain is the output, and the emitter or source is common to both input and output (it may be tied to the ground reference or the power supply rail), which gives rise to its common name.

Figure 9.2: Basic n-type inverting voltage amplifier circuit (neglecting biasing details)

The common emitter or source amplifier may be viewed as a transconductance amplifier ( i.e. voltage in, current out) or as a voltage amplifier (voltage in, voltage out). As a transconductance amplifier, the small signal input voltage, v be for a BJT or v gs for a FET, times the device transconductance g m , modulates the amount of current flowing through the transistor, i c or i d . By passing this varying current through the output load resistance, R L it will be converted back into a voltage V out . However, the transistor’s small signal output resistance, r o , is not typically high enough for a reasonable transconductance amplifier (ideally infinite). Nor is the output load, R L , low enough for a decent voltage amplifier (ideally zero). Another major drawback is the amplifier’s limited high-frequency response due in part to the built in collector base or drain gate capacitance inherent to the transistor. More on how this capacitance effects the frequency response in a later section of this chapter. Therefore, in practice the output often is routed through either a voltage follower (common collector or drain stage), or a current follower (common base or gate stage), to obtain more favorable output and frequency characteristics. This latter combination is called a cascode amplifier as we will see later in the chapter on multi-stage amplifiers.

In comparison to the BJT common emitter amplifier, the FET common source amplifier has higher input impedance. The generally lower g m of the FET vs. the BJT at equal current levels leads to lower voltage gain for the MOS version.

In order for the common emitter or source amplifier to provide the largest output voltage swing, the voltage at the Base or Gate terminal of the transistor is offset in such a way that the transistor is nominally operating halfway between its cut-off and saturation points. Note the NMOS (a) and NPN (b) characteristic curves in figure 9.2.1. This allows the amplifier stage to more accurately reproduce the positive and negative halves of the input signal superimposed upon the DC Bias voltage. Without this offsetting Bias Voltage only the positive half of the input waveform would be amplified.

Figure 9.2.1 (a) I D vs. V DS curves and (b) I C vs. V CE curves

The red line superimposed on the two sets of curves represents the DC load line of a 400 ohm R L . To maximize the output swing it is desirable to set the operating point of the transistor, with a zero input signal, at a drain or collector voltage of one half the supply voltage, which would be 4 volts in this case. Finding the corresponding drain or collector current along the load line gives us the target current level. This is around 10mA for R L equal to 400 ohms. The next step is to determine the corresponding V GS or I B for a 10mA I D or I C . In the NMOS example each curve represents a different V GS from 0.9 volts to 1.5 volts in 0.1 volt steps. The NMOS device used in this example has a transconductance of about 40mA/ V . The I D equal to 10mA point on the load line falls between the 1.4V and 1.3V curves or a V GS of 1.32V. In the NPN example each curve represents a different I B from 10uA to 100uA in 10uA steps. The 50uA curve happens to cross the load line at I C =10mA. The β of the transistor must therefore be about 200. The task now is to somehow provide this DC offset or bias at the Gate or Base of the transistor.

The first bias technique we will explore is called voltage divider bias and is shown in figure 9.2.2. If we choose the correct resistor values for R 1 and R 2 that will result in a collector or drain current such that one half of the supply voltage, V + appears across R L we should have our desired value of V GS or V BE (I B ) for biasing with no signal input. For the MOS case we know that no current flows into the gate so the simple voltage divider ratio can be used to pick R 1 and R 2 . If V + = 8V and we want V GS to equal 1.32 V then:

The actual values of R 1 and R 2 are not so important just their ratio. However, the divider ratio we choose will be correct for only one set of conditions of power supply voltage, transistor threshold voltage and transconductance, and temperature. Actual designs often use more involved bias schemes.

Figure 9.2.2 Voltage divider bias

For the NPN case the calculation is somewhat more involved. We know we want I B to be equal to 50uA. The current that flows in R 1 is the sum of the current in R 2 and I B which puts an upper bound on R 1 when R 2 is infinite and no current flows in R 2 . If we assume a nominal V BE of 0.65 volts then R 1 must be no larger than 7.35V/50uA or 147KΩ. The purpose of the voltage divider is to attenuate the variations in V + and thus make the DC operating point of the transistor less sensitive to V +. To that end we need to make the current in R 2 many times larger than I B . If we, for example, choose to make I R2 9 times I B then the current in R 1 will be 10*I B or 500uA. R 1 will be 1/10 what we just calculated as the upper bound or 14.7KΩ. R 2 will be V BE divided by 450uA or 1.444KΩ which is a divider ratio of 0.8921. If we had simply used 8V- V BE /8V as the ratio (assume V BE = 0.65V) the divider ratio would have been 0.8125. Taking I B into account shifted the required ratio. These values would need to be adjusted slightly if the actual V BE was not the 0.65 volts (or β was not 200) we used in this calculation. This points out a major limitation of this bias scheme as we pointed out in the MOS example above. That is the sensitivity to device specific characteristics like V BE and β as well as supply voltage and temperature.

A consequence of including this bias scheme is a lowering of the input impedance. The input now includes the parallel combination of R 1 and R 2 across the input. For the MOS case this now sets the input resistance. For the BJT case we now have R 1 ||R 2 ||r π as the effective input resistance.

There is another minor inconvenient problem with this bias scheme when it is connected to a prior stage in the signal path. This bias configuration places the AC input signal source directly in parallel with R 2 of the voltage divider. This may not be acceptable, as the input source may tend to add or subtract from the DC voltage dropped across R 2 .

One way to make this scheme work, although it may not be obvious why it will work, is to place a coupling capacitor between the input voltage source and the voltage divider as in figure 9.2.3 below.

Figure 9.2.3 Coupling capacitor C C prevents voltage divider bias current from flowing into the input signal source.

The capacitor forms a high-pass filter between the input source and the DC voltage divider, passing almost the entire AC portion of the input signal on to the transistor while blocking all the DC bias voltage from being shorted through the input signal source. This makes much more sense if you understand the superposition theorem and how it works. According to superposition, any linear, bilateral circuit can be analyzed in a piecemeal fashion by only considering one power source at a time, then algebraically adding the effects of all power sources to find the final result. If we were to separate the capacitor and the R 1 /R 2 voltage divider circuit from the rest of the amplifier, it might be easier to understand how this superposition of AC and DC would work.

With only the AC signal source in effect, and a capacitor with an arbitrarily low impedance at the input signal frequency, almost all the AC voltage appears across R 2 .

To calculate the small signal voltage gain of the common emitter or source amplifier we need to insert a small signal model of the transistor into the circuit. The small signal models of the BJT and MOS FET are actually very similar so the gain calculation for either version is much the same. The small signal hybrid-π models for the BJT and MOS amplifiers are shown in figure 9.2.4.

Figure 9.2.4 Common emitter or source small signal models.

The following are some of the key model equations we will need to calculate the amplifier stage voltage gain. These equations are used for the other amplifier configurations that we will discuss in following sections as well.

The small signal voltage gain A v is the ratio of the input voltage to the output voltage:

The input voltage V in (v be for the BJT and v gs for the MOS) times the transconductance g m is equal to the small signal output current, i o in the collector or drain. V out will be simply this current times the load resistance R L, neglecting the small signal output resistance r o for the moment. Notice the minus sign because of the direction of the current i o .

Rearranging for the gain we get:

Substituting the BJT and MOS g m equations we get:

Comparing these two gain equations we see that they both depend on the DC collector or drain currents. The BJT gain is inversely proportional to V T (the Thermal Voltage) which is approximately 26mV at room temperature. The Thermal Voltage, V T increases with increasing temperature so from the equation we see that the gain will actually decrease with increasing temperature. The MOS gain is inversely proportional to the over drive voltage, V ov ( V GS – V th ) which is often much larger than V T at similar drain currents leading to the lower gain for the MOS stage vs. the BJT stage for approximately equal bias currents.

If R L is relatively large when compared to the small signal output resistance then the gain will be reduced because the actual output load is the parallel combination of R L and r o . In fact r o puts an upper bound on the possible gain that can be achieved with a single transistor amplifier stage.

Again looking at the small signal models in figure 9.2.4 we see that for the BJT case the input V in will see r π as a load. For the MOS case V in will see basically an open circuit (for low frequencies anyway). This will of course be the case absent any Gate or Base bias circuitry.

Again looking at the small signal models in figure 9.2.4 we see that for both the BJT case and the MOS case the output impedance is the parallel combination of R L and r o . For most practical applications we can ignore r o because it is very often much larger than R L . Below are the BJT and MOS r o equations.

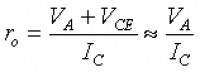
ADALM1000 Lab Activity 5, Common emitter amplifier ADALM1000 Lab Activity 5M, Common source amplifier

ADALM2000 Lab Activity 5, Common emitter amplifier ADALM2000 Lab Activity 5M, Common source amplifier ADALM2000 Lab Activity 5FR, Amplifier Frequency Response

9.3 The Current Follower also known as Common base or gate amplifier

The Current Follower or Common base/gate amplifier has a high voltage gain, relatively low input impedance and high output impedance compared to the voltage follower or common collector/drain amplifier. The BJT and MOS versions are shown in figure 9.3

Figure 9.3: Basic n-type current follower or common base/gate circuit (neglecting biasing details)

In applications where only a positive power supply voltage is provided some means of providing the necessary DC voltage level for the common gate or base terminal is required. This might be as simple as a voltage divider between ground and the supply. In applications where both positive and negative supply voltages are available, ground is a convenient node to use for the common gate or base terminal.

The common gate or base stage is most often used in combination with the common emitter or source amplifier in what is known as the cascode configuration. The cascode will be covered in the next chapter on multi stage amplifiers in greater detail.

To calculate the small signal voltage gain of the common base or gate amplifier we insert the small signal model of the transistor into the circuit. The small signal models for the BJT and MOS amplifiers are shown in figure 9.3.1.

Figure 9.3.1 Current follower or Common base/gate small signal models.

Much like in the common emitter/source amplifier stage the small signal input voltage, V in (v be for the BJT and v gs for the MOS) times the transconductance g m is equal to the small signal output current, i o in the collector or drain. V out will be simply this current times the load resistance R L, neglecting the small signal output resistance r o for the moment.

It is perhaps more useful to consider the current gain of the current follower stage rather than its voltage gain. In the case of the MOS version we know that I S = I D because I G = 0. Thus the MOS stage current gain is exactly 1. In the case of the BJT version we know that the ratio of I C to I E is equal to α and thus will be slightly less than 1.

Again looking at the small signal models in figure 9.3.1 we see that for the BJT case the input V in will see r π in parallel with the series combination of g m and R L as a load. For the MOS case V in will see basically just the series combination of g m and R L . The equation below (from the BJT small signal T model) relates g m and the resistance seen at the emitter r E . We can also use this relationship to give us the resistance seen at the source r S .

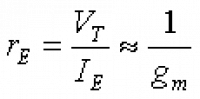
It is also important to note here that 100% (neglecting I B in the BJT case) of the current from the input source flows through the transistor and becomes the output current. Thus the name current follower.

Again looking at the small signal models in figure 9.3.1 we see that for both the BJT case and the MOS case the output impedance is the parallel combination of R L and r o . We can generally assume this is true if we consider that V in is driven from a low impedance (nearly ideal) voltage source. If this is not the case then the finite output impedance must be added in series with r o . If the input of the current follower is driven by the relatively high output impedance of a transconductance amplifier such as the common emitter or source amplifier from earlier then the output impedance for the combined amplifier can be very high. For most practical applications we can ignore r o because it is very often much larger than R L .

ADALM1000 Lab Activity, BJT Common Base Amplifier ADALM1000 Lab Activity, BJT Common Gate Amplifier ADALM1000 Lab Activity, Folded Cascode Amplifier

The Emitter or Source follower is often called a common Collector or Drain amplifier because the collector or drain is common to both the input and the output. This amplifier configuration, figure 9.4, has its output taken from the emitter/source resistor and is useful as an impedance matching device since its input impedance is much higher than its output impedance. The voltage follower is also termed a “buffer” for this reason.

Figure 9.4:Basic n-type Voltage follower or common collector/drain circuit (neglecting biasing details)

The gain of the voltage follower is always less than one since r E and R L or r S and R L form a voltage divider. The input to output offset is set by the V BE drop of about 0.65 volts below the base for the BJT and V GS below the gate for the MOS. This configuration’s function is not voltage gain but current or power gain and impedance matching. The input impedance is much higher than its output impedance so that a signal source does not have to supply as much power to the input. This can be seen from the fact that the base current is on the order of 100 times (β) less than the emitter current. The low output impedance of the emitter follower matches a low impedance load and buffers the signal source from that low impedance.

The collector/source current is basically determined by the emitter/source resistor so the main design variables in this case is simply R L and the power supply voltage.

To calculate the small signal voltage gain of the voltage follower configuration we insert the small signal model of the transistor into the circuit. The small signal models for the BJT and MOS amplifiers are shown in figure 9.4.1.

Figure 9.4.1 Voltage Follower small signal models.

For the circuit in figure 9.4.2 calculate the voltage gain A V = V out / V in .

Figure 9.4.2 BJT Voltage gain example

To use the voltage gain formula we just obtained using the small signal models we need to first calculate r E . From section 9.3.3 we are given the equation for r E :

To use this formula we need to know I E . We know that the voltage across R L is V out . We also know that V out = V in - V BE . If we use an estimate of V BE to be 0.6 volts, we get V out = 5.6 - 0.6 or 5 volts. If R L is 1KΩ then I E is 5mA. Using a room temperature value for V T = 25mV, we get r E is equal to 5Ω. Substituting these values into our gain equation we get:

The output impedance is simple the parallel combination of the Emitter (Source) resistor R L and the small signal emitter (source) resistance of the transistor r E . Again from section 9.3.3, the equation for r E is as follows:

Similarly, the small signal source resistance, r S , for a MOS FET is 1/ g m .

Referring back to our gain example in figure 9.4.2, we can also calculate the output resistance, which will be the parallel combination of the 1KΩ R L and the 3Ω r E or 2.99Ω.

ADALM1000 Lab Activity 11, BJT Emitter follower ADALM1000 Lab Activity 11M, MOS Source follower

ADALM2000 Lab Activity 11, BJT Emitter follower ADALM2000 Lab Activity 11m, MOS Source follower

9.5 Series Feedback: emitter/source degeneration

Common emitter/source amplifiers give the amplifier an inverted output and can have a very high gain and can vary widely from one transistor to the next. The gain is a strong function of both temperature and bias current, and so the actual gain is somewhat unpredictable. Stability is another problem associated with such high gain circuits due to any unintentional positive feedback that may be present. Other problems associated with the circuit are the low input dynamic range imposed by the small-signal limit; there is high distortion if this limit is exceeded and the transistor ceases to behave like its small-signal model. When negative feedback is introduced, many of these problems are reduced, resulting in improved performance. There are several ways to introduce feedback in this simple amplifier stage, the easiest and most reliable of which is accomplished by introducing a small value resistor in the emitter circuit (R E ). This is also referred to as series feedback. The amount of feedback is dependent on the relative signal level dropped across this resistor. The signal seen across R E is out of phase with the signal seen at V out and thus subtracts from V out reducing its amplitude. When the emitter resistor value approaches that of the collector load resistor (R L ), the gain will approach unity (A v ~ 1).

Figure 9.5: Adding an emitter/source resistor decreases gain. However, with increased linearity and stability

It is much less common to include a degeneration resistor in MOS designs. This is because, in microelectronic integrated circuits, the gain ( g m ) of the device can be adjusted by changing the W/L ratio. This degree of design freedom is not generally available in Bipolar (BJT) processes.

DC Biasing example with emitter degeneration

There are some BJT biasing rules of thumb:

1. Set I E not I B or V BE : less dependence on β and temperature ( V T ) 2. Allow 1/3V CC across R C , V CE and R B2 3. Save power by allowing only 10% of I E in R B

We are given the following for circuit in figure 9.5.1, V CC = 20V ; I E = 2mA ; β = 100. From our rules of thumb we set V B = 1/3* V CC = 6.7 V .

Figure 9.5.1 DC Biasing example

V B = (R B2 /(R B1 +R B2 ))* V CC ⇒ 6.7V = (R B2 /(R B1 +R B2 ))*20 (1)

V CC /(R B1 + R B2 ) = 0.1*I E ⇒ 20/(R B1 + R B2 ) = 200 μA (2)

Solving equations (1) and (2) we get:

R B1 =2R B2 then from (2)

3R B2 = 20/200 μA = 100kΩ

So, R B2 = 33kΩ and R B1 = 66kΩ

Now we have V E = V B – V BE = 6.7 – 0.7 = 6 V and I E is 2 mA : R E = V E /I E = 6/2mA = 3kΩ.

I C = (β/(β+1))*I E = (100/101)*2mA = 1.98 mA and I B = I C /β = 1.98mA/100 = 19.8μA.

From our rules of thumb we know that V C = 2/3*20V = 13.3 V

So to find R L we have: R L = ( V CC – V C )/I C = (20 – 13.3)/1.98mA = 3.4kΩ

To calculate the small signal voltage gain of the common emitter/source amplifier with the addition of emitter/source degeneration we again insert the small signal model of the transistor into the circuit. The small signal models for the BJT and MOS amplifiers are shown in figure 9.5.1.

Figure 9.5.1 Common emitter/source with degeneration

The impedance R E reduces the overall transconductance g m of the circuit by a factor of g m R E + 1, which makes the voltage gain:

So the voltage gain depends almost exclusively on the ratio of the resistors R L / R E rather than the transistor’s intrinsic and unpredictable characteristics. The distortion and stability characteristics of the circuit are thus improved at the expense of a reduction in gain.

Going back to our earlier biasing example, figure 9.5.1, values for I C = 2mA, R L = 3.4KΩ and R E = 3KΩ to calculate the small signal gain we first find g m = I C / V T = 2mA/25mV = 0.08. Using our formula for A V :

Again looking at the small signal models in figure 9.4.1 we see that for the BJT case the input V in see r  in series with degeneration resistor R E as a load. For the MOS case V in see basically an open circuit.

Again looking at the small signal models in figure 9.5.1 we see that for both the BJT case and the MOS case, much like in the earlier common emitter/source stage, the output impedance is the parallel combination of R L and r o but now degeneration resistor R E is in series with r o . For most practical applications we can ignore r o because it is very often much larger than R L .

Basically the same techniques used in the simple common emitter/source amplifier stage, which were discussed in section 9.2.1, can be used when the emitter degeneration resistor is added. The added voltage across the R E (R E *I E ) must be added to the bias level. This added voltage drop actually make the operating point (I C ) much less sensitive to the bias level.

The small signal voltage gain of the common emitter amplifier with the emitter resistance is approximately R L / R E . For cases when a gain larger than 5-10 is needed, R E may be become so small that the necessary good biasing condition, V E = R E *I E > 10* V T cannot be achieved. A way to restore the small signal voltage gain while maintaining the desired DC operating bias is to use a by-pass capacitor as is figure 9.5.4. The small AC signal sees an emitter resistance of just R E1 while for DC bias the emitter resistance is the series combination of R E = R E1 +R E2 . Calculations for the common emitter amplifier with emitter degeneration can be applied here by replacing R E with R E1 when deriving the amplifier gain, and input and output impedances, because a sufficiently large bypass capacitor in effects shorts R E2 and is effectively removed from the circuit for sufficiently high frequency inputs.

Figure 9.5.4 addition of emitter by-pass capacitor

Using our earlier biasing exercise in figure 9.5.1 as an example but splitting the 3KΩ R E into two resistors as in figure 9.5.4 with R E1 = 1KΩ and R E2 = 2KΩ with C 1 = 1uF we can recalculate the small signal gain for high frequencies, where C 1 effectively shorts out R E2 , to be:

The addition of by-pass capacitor C 1 , however, modifies the low frequency response of the circuit. We know from our two gain calculations that the DC gain of the circuit is -1.13 and the gain increases to -3.36 for high frequencies. We can therefore assume that the frequency response consists of a relatively low frequency zero followed by a somewhat higher frequency pole. The formulas for the zero and pole are as follows:

where R’ E = R E2 || (R E1 + r e )

For our example problem with R E1 = 1K , R E2 = 2K and C 1 = 1uF we get the frequency for the zero equal to 80 Hz and the frequency for the pole equal to 237 Hz. The simulated frequency response from 1 Hz to 100 KHz for the example circuit is shown in figure 9.5.5.

Figure 9.5.5 simulated frequency response

1. Find DC operating point. 2. Calculate small-signal parameters: g m , r  , r e etc. 3. Replace DC voltage sources with AC grounds and DC current sources with open circuits. 4. Replace transistor with small-signal model (hybrid-π model or T model)

At this point we are going to take a diversion to discuss Miller’s Theorem. While the methods we have been using up to this point are completely general, there are certain configurations that lend themselves to be analyzed more simply by Miller’s Theorem. Miller’s theorem states that in a linear circuit, if there is a branch where an impedance Z, connects two nodes with node voltages V 1 and V 2 , this branch can be replaced by two other branches connecting the corresponding nodes to ground by impedances respectively Z / (1- K ) and KZ / ( K -1), where the gain from node 1 to node 2 is K = V 2 / V 1 .

Figure 9.6.1 Miller’s Theorem

At this point we will go through the steps that show how the Miller impedances are arrived at. We can use the equivalent two-port network technique to replace the two-port represented in figure 9.6.1(a) to its equivalent in figure 9.6.2.

Figure 9.6.2

Replacing the voltage sources in figure 9.6.2 with their Norton equivalent current sources we get figure 9.6.3.

Figure 9.6.3

Using the source absorption theorem (see the Appendix at the end of this chapter), we get figure 9.6.4.

Figure 9.6.4

Which gives us figure 9.6.5 (which is figure 9.6.1(b) ) when we parallel combine the two impedances.

Figure 9.6.5

9.7 Shunt feedback:

Another biasing technique for the common emitter or source amplifier, called shunt feedback, is accomplished by the introduction of some fraction of the collector or drain signal back to the input at the base or gate. This is done via the biasing resistor (R F ), as shown in figure 9.7.1. Resistor R F connects between two nodes that have gain, A V ( K ), between them and thus the application of Miller’s theorem is the best way analyze the small signal characteristics of this circuit.

Figure 9.7.1 Drain-to-Gate (a) and Collector-to-Base (b) shunt feedback

Figure 9.7.1(a) shows a common source NMOS amplifier using drain feedback biasing. This type of biasing is often used with enhancement mode MOSFETS and can be useful when operating with a low voltage power supply ( V + ). If Vin is AC coupled, the voltage on the gate is equal to the voltage on the drain ( V GS = V DS ) since no gate current flows through R F . If Vin is DC coupled then a voltage divider is formed by R F and R S and V GS will be less than V DS . It is useful to note that the transistor is always in saturation when V GS = V DS . If the drain current increases for some reason, such as a change in V + , the gate voltage drops. The decreased gate voltage in turn causes the drain current to decreases which causes the gate voltage to increase. The negative feedback loop reaches an equilibrium that is the bias point for the circuit.

Some data sheets for enhancement MOSFETS give a value for I D (on), where V GS = V DS lf I D (on) is known, the circuit component can be easily calculated as shown in Example 9.3. The input impedance of a circuit using drain feedback biasing is equal to the value of R F divided by the voltage gain plus one.

This configuration employs negative feedback to stabilize the operating point. In this form of biasing, the base feedback resistor R F is connected to the collector instead of connecting it to the DC source V + . So any large increase in the collector current will induce a voltage drop across the R L resistor that will in turn reduce the transistor’s base current.

If we assume that the input source Vin is AC coupled and no DC bias current flows in R S , from Kirchhoff’s voltage law, the voltage V RF across the base resistor R F is:

By the Ebers–Moll model, I c = βI b , and so:

From Ohm’s law, the base current I b = V RF /R F , and so:

Hence, the base current I b is:

If V BE is held constant and temperature increases, then the collector current I c increases. However, a larger I c causes the voltage drop across resistor R L to increase, which in turn reduces the voltage V RF across the base resistor R F . A lower base-resistor voltage drop reduces the base current I b , which results in less collector current I c . Because an increase in collector current with temperature is opposed, the operating point is kept more stable.

• Circuit stabilizes the operating point against variations in temperature and β (ie. Transistor process variations)
• In this circuit, to keep I c independent of β, the following condition must be met:

which is the case when:

• As β is fixed (and generally not known precisely) for a given transistor, this relation can be satisfied either by keeping R L fairly large or making R F very low.
• If R L is large, a high V + is necessary, which increases cost as well as precautions necessary while handling.
• If R F is low, the reverse bias of the collector–base region is small, which limits the range of collector voltage swing that leaves the transistor in active mode.
• The resistor R F causes an AC feedback, reducing the voltage gain of the amplifier. This undesirable effect is a trade-off for greater quiescent operating point stability.

Usage: The feedback also decreases the input impedance of the amplifier as seen from the base, which can be advantageous. Due to the gain reduction from feedback, this biasing form is used only when the trade-off for stability is warranted.

For the amplifier shown in figure 9.7.2(a) with a DC coupled input source V in calculate the input and output resistance and voltage gain A V . We first need to start with some preliminary DC analysis to determine the operating point of Q 1 . For this we set V in to zero volts, i.e. short it out. If we assume a V BE of 0.65 volts we will have 65 uA flowing in the 10K resistor R S . Given that V + is 10V, we would like V out to be 5 volts. The current in R L is equal to 500uA and will split between the collector of Q 1 and the feedback resistor R F . The voltage across the 62.7KΩ feedback resistor is 5-0.65 or 4.35 volts. The current in R F splits between the current in R S and I B . The base current I B is equal to 4.35/62.7KΩ – 65uA or 4.3 uA. We should get a collector current of 500uA - 69.3uA or 430.3uA with a β of about 100.

If we use Miller’s theorem to replace the feedback resistor R F with its two equivalent impedances we get figure 9.7.2(b). Assuming that the voltage gain from base to collector A V is significantly greater than 1 we can make the simplification that A V /(A V -1) is close to 1. The effective load resistance, R Leq we will use to calculate the gain will be 10KΩ||62.7KΩ or 8.62KΩ. Now we can use the same common emitter or source small signal gain equations we used in section 9.2.2. The 430uA collector currents gives us a g m of 430uA/25mV or 0.0172. We know that A V = - g m R Leq or A V = -0.0172*8.62K = -148 which is » 1. The input resistance seen at the base of Q 1 will be the r π of Q 1 , which is equal to β/ g m or 100/0.0172 = 5.814KΩ, in parallel with the Miller resistance 62.7KΩ/149 = 421Ω thus the effective input resistance, R base will be about 392.5Ω.

Figure 9.7.2 Example using Miller’s theorem

The input source resistance R S and the equivalent resistance at the base, R base form a voltage divider. To calculate the overall voltage gain from voltage source V in to V out we multiply this divider ratio times the base to collector gain, A V we just calculated.

From our investigation of the inverting op amp configuration in Chapter 3 we learned that for amplifiers with less than infinite gain the actual gain will be less than the ideal gain equation, Gain = -R F /R S predicts. If our single transistor amplifier had infinite gain the gain from V in to V out would be 62.7KΩ/10KΩ or 6.27. In Chapter 3 we got an estimation of the percentage error, ε, due to finite gain A V (remember β in this equation is the feedback factor not the current gain of the transistor):

The actual gain of 5.6 is about 10% smaller than the ideal gain of 6.27.

Part 1 DC operating point:

For the circuit in figure 9.7.3 calculate the required R F to bias the DC operating point such that V out is equal to ½ the supply voltage or +5V when Vin = 0. Assume V BE = 0.65V and β = 200.

Figure 9.7.3

Part 2 Small signal gain and impedance:

Given the value for R F calculated in part 1 calculate the voltage gain A V , the input resistance R base and the output resistance R out . Also calculate the overall voltage gain V out / V in and explain why this is different than the ideal value of –R F /R S .

The Miller effect is key to predicting the frequency response of an inverting amplifier stage where capacitive feedback is included. Typically there’s a low-pass pole in the voltage gain stage created by R S of the signal source and a feedback capacitor C C . But, the low pass cutoff is not simply determined by R S and C C . The Miller effect creates an effective capacitance at the base/gate of the transistor that appears as C C scaled by the amplifier’s voltage gain.

Figure 9.7.3 Miller feedback capacitor

The Miller effect is especially useful when you’re trying to produce a low-pass filter on an IC op amp with a relatively low frequency cut-off. The difficulty is that large capacitors are difficult to make because they take up so much space on the IC. The solution is to make a small capacitor and then scale up its behavior using the Miller effect.

Equivalent Circuit

Here’s a simplified version of the circuit above.

Figure 9.7.4 Miller feedback equivalent circuit

Miller said that you can approximate the input capacitance by replacing C C with a different capacitance C M across the R IN . How much bigger is C M ? C C is multiplied by the voltage gain (A V = g m R L ) of the amplifier. Miller’s theorem also states there will be a capacitor C’ C across R L that is equal to C C times (A V +1)/A V which for large values of A V we assume to be 1.

How does this work? Well, we know that forcing a voltage across a capacitor causes a current to flow. How much current depends on the capacitance: I = C C · ΔV/Δt. However, in this circuit, the voltage gain at R L causes a much larger ΔV across C C - causing an even larger current to flow through C C . Therefore, it looks like a much larger capacitance from the point of view of V IN .

In this example we will use the circuit shown in figure 9.7.5 to illustrate the Miller multiplication of the feedback capacitor C C . Bias resistors R 1 and R S are chosen to set the DC operating point such that V out is at a DC value of approximately V +/2 or 5V. With the given R L of 10KΩ the low frequency small signal voltage gain A V is approximately 80.

We can now calculate the -3 dB frequency and unity gain (0dB) frequency for a feedback capacitor, C C , of 0.001 uF. The frequency where the gain from V in to V out falls by -3 dB from its DC values is approximately equal to:

The unity gain frequency is approximately equal to :

Figure 9.7.5 Miller Capacitance Example

The circuit in figure 9.7.5 was simulated and the AC frequency response from 1 Hz to 1 MHz is plotted in figure 9.7.6. The gain from V in to V out in dB is 20Log(A V ) or about 38 dB . The -3 dB frequency in this case would be where the gain curve crosses 35 dB (~263 Hz) and the unit gain frequency would be where the gain curve crosses the 0 dB line (~21.7 KHz ). The simulation results are in reasonably close agreement with our approximate hand calculations. For our hand calculations we assumed that R 1 was sufficiently larger than R S so it could be ignored and likewise the r π of Q 1 was large enough to not materially affect R S .

Figure 9.7.6 Frequency sweep simulation

Chapter Summary:

• The Common Emitter stage has high gain but low input and high output impedance.
• R E emitter degeneration improves input impedance and provides negative feedback to stabilize DC operating point but with some loss in gain.
• The Common Base stage has low input, high output impedance but is good at high frequencies. Good current buffer sometimes called the current follower.
• The Common Collector or Emitter follower can be biased with large input impedance, low output impedance but has approximately unity gain. Good voltage buffer.

The source absorption theorem has two dual forms: the voltage source absorption and the current source absorption theorems.

The voltage source absorption theorem states that if, in one branch of the circuit with current I, there is a voltage source controlled by I, the source can be replaced by a simple impedance with value equal to the source controlling factor.

Figure 9A.1

The proof is trivial. An impedance Z where a current I flows has the same voltage drop the I controlled source generates at its terminals.

The current source absorption theorem states that if, in one branch of the circuit there is a current source controlled by a voltage V , the source can be replaced by a simple admittance with value equal to the source controlling factor.

Figure 9A.2

The proof is again trivial. An admittance Y submitted to a voltage V imposes the same current that the source Y V provides.

Figure A9.3 shows the small signal equivalent circuit model of a transistor. Find the resistance Rin looking into the emitter (with base and collector at small signal AC grounds).

Figure 9A.3

Using what we just learned about the source absorption theorem for current sources we know we can replace the controlled source with a resistance equal to 1/ g m its transconductance.

Advanced Topics:

Figure AT1.1 Inserting a Diode connected device in the bias divider

Figure AT1.2 Inserting R 2 increases the input resistance

Return to Previous Chapter

Go to Next Chapter

Return to Table of Contents

• View Source
• Fold/unfold all
• [ Back to top ]