p value in hypothesis testing

• Data Science
• Data Science Projects
• Data Analysis
• Data Visualization
• Machine Learning
• ML Projects
• Deep Learning
• Computer Vision
• Artificial Intelligence

P-Value: Comprehensive Guide to Understand, Apply, and Interpret

A p-value is a statistical metric used to assess a hypothesis by comparing it with observed data.

This article delves into the concept of p-value, its calculation, interpretation, and significance. It also explores the factors that influence p-value and highlights its limitations.

Table of Content

• What is P-value?

How P-value is calculated?

How to interpret p-value, p-value in hypothesis testing, implementing p-value in python, applications of p-value, what is the p-value.

The p-value, or probability value, is a statistical measure used in hypothesis testing to assess the strength of evidence against a null hypothesis. It represents the probability of obtaining results as extreme as, or more extreme than, the observed results under the assumption that the null hypothesis is true.

In simpler words, it is used to reject or support the null hypothesis during hypothesis testing. In data science, it gives valuable insights on the statistical significance of an independent variable in predicting the dependent variable. 

Calculating the p-value typically involves the following steps:

• Formulate the Null Hypothesis (H0) : Clearly state the null hypothesis, which typically states that there is no significant relationship or effect between the variables.
• Choose an Alternative Hypothesis (H1) : Define the alternative hypothesis, which proposes the existence of a significant relationship or effect between the variables.
• Determine the Test Statistic : Calculate the test statistic, which is a measure of the discrepancy between the observed data and the expected values under the null hypothesis. The choice of test statistic depends on the type of data and the specific research question.
• Identify the Distribution of the Test Statistic : Determine the appropriate sampling distribution for the test statistic under the null hypothesis. This distribution represents the expected values of the test statistic if the null hypothesis is true.
• Calculate the Critical-value : Based on the observed test statistic and the sampling distribution, find the probability of obtaining the observed test statistic or a more extreme one, assuming the null hypothesis is true.
• Interpret the results: Compare the critical-value with t-statistic. If the t-statistic is larger than the critical value, it provides evidence to reject the null hypothesis, and vice-versa.

Its interpretation depends on the specific test and the context of the analysis. Several popular methods for calculating test statistics that are utilized in p-value calculations.

In general, a small p-value indicates that the observed data is unlikely to have occurred by random chance alone, which leads to the rejection of the null hypothesis. However, it’s crucial to choose the appropriate test based on the nature of the data and the research question, as well as to interpret the p-value in the context of the specific test being used.

The table given below shows the importance of p-value and shows the various kinds of errors that occur during hypothesis testing.

Type I error: Incorrect rejection of the null hypothesis. It is denoted by α (significance level). Type II error: Incorrect acceptance of the null hypothesis. It is denoted by β (power level)

Let’s consider an example to illustrate the process of calculating a p-value for Two Sample T-Test:

A researcher wants to investigate whether there is a significant difference in mean height between males and females in a population of university students.

Suppose we have the following data:

Starting with interpreting the process of calculating p-value

Step 1 : Formulate the Null Hypothesis (H0):

H0: There is no significant difference in mean height between males and females.

Step 2 : Choose an Alternative Hypothesis (H1):

H1: There is a significant difference in mean height between males and females.

Step 3 : Determine the Test Statistic:

The appropriate test statistic for this scenario is the two-sample t-test, which compares the means of two independent groups.

The t-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

• s1 = First sample’s standard deviation
• s2 = Second sample’s standard deviation
• n1 = First sample’s sample size
• n2 = Second sample’s sample size

So, the calculated two-sample t-test statistic (t) is approximately 5.13.

Step 4 : Identify the Distribution of the Test Statistic:

The t-distribution is used for the two-sample t-test . The degrees of freedom for the t-distribution are determined by the sample sizes of the two groups.

 The t-distribution is a probability distribution with tails that are thicker than those of the normal distribution.

• where, n1 is total number of values for 1st category.
• n2 is total number of values for 2nd category.

The degrees of freedom (63) represent the variability available in the data to estimate the population parameters. In the context of the two-sample t-test, higher degrees of freedom provide a more precise estimate of the population variance, influencing the shape and characteristics of the t-distribution.

T-Statistic

The t-distribution is symmetric and bell-shaped, similar to the normal distribution. As the degrees of freedom increase, the t-distribution approaches the shape of the standard normal distribution. Practically, it affects the critical values used to determine statistical significance and confidence intervals.

Step 5 : Calculate Critical Value.

To find the critical t-value with a t-statistic of 5.13 and 63 degrees of freedom, we can either consult a t-table or use statistical software.

We can use scipy.stats module in Python to find the critical t-value using below code.

Comparing with T-Statistic:

The larger t-statistic suggests that the observed difference between the sample means is unlikely to have occurred by random chance alone. Therefore, we reject the null hypothesis.

• p ≤ (α = 0.05) : Reject the null hypothesis. There is sufficient evidence to conclude that the observed effect or relationship is statistically significant, meaning it is unlikely to have occurred by chance alone.
• p > (α = 0.05) : reject alternate hypothesis (or accept null hypothesis). The observed effect or relationship does not provide enough evidence to reject the null hypothesis. This does not necessarily mean there is no effect; it simply means the sample data does not provide strong enough evidence to rule out the possibility that the effect is due to chance.

In case the significance level is not specified, consider the below general inferences while interpreting your results. 

• If p > .10: not significant
• If p ≤ .10: slightly significant
• If p ≤ .05: significant
• If p ≤ .001: highly significant

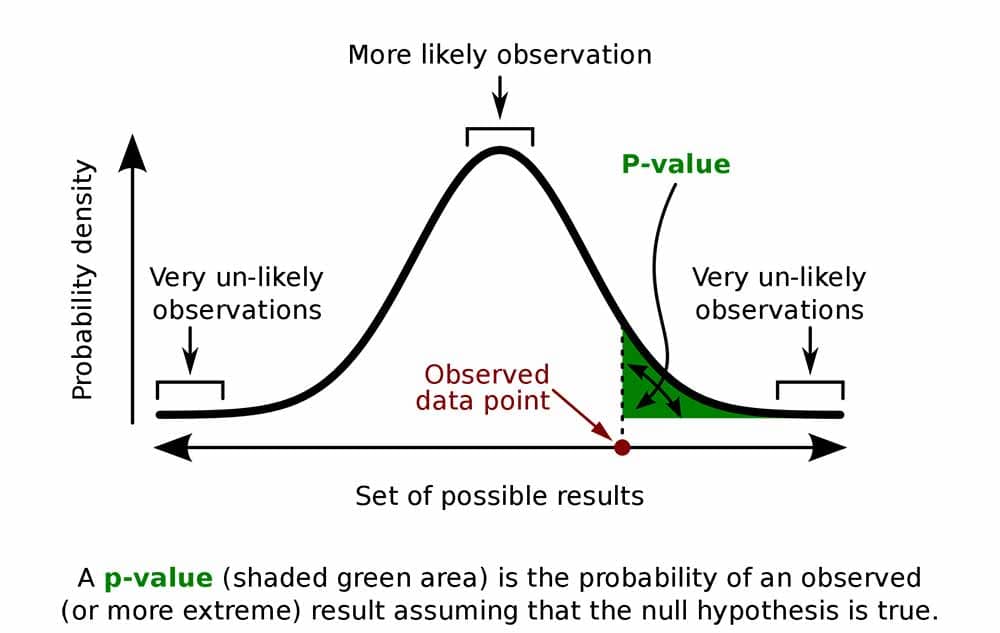
Graphically, the p-value is located at the tails of any confidence interval. [As shown in fig 1]

Fig 1: Graphical Representation 

What influences p-value?

The p-value in hypothesis testing is influenced by several factors:

• Sample Size : Larger sample sizes tend to yield smaller p-values, increasing the likelihood of detecting significant effects.
• Effect Size: A larger effect size results in smaller p-values, making it easier to detect a significant relationship.
• Variability in the Data : Greater variability often leads to larger p-values, making it harder to identify significant effects.
• Significance Level : A lower chosen significance level increases the threshold for considering p-values as significant.
• Choice of Test: Different statistical tests may yield different p-values for the same data.
• Assumptions of the Test : Violations of test assumptions can impact p-values.

Understanding these factors is crucial for interpreting p-values accurately and making informed decisions in hypothesis testing.

Significance of P-value

• The p-value provides a quantitative measure of the strength of the evidence against the null hypothesis.
• Decision-Making in Hypothesis Testing
• P-value serves as a guide for interpreting the results of a statistical test. A small p-value suggests that the observed effect or relationship is statistically significant, but it does not necessarily mean that it is practically or clinically meaningful.

Limitations of P-value

• The p-value is not a direct measure of the effect size, which represents the magnitude of the observed relationship or difference between variables. A small p-value does not necessarily mean that the effect size is large or practically meaningful.
• Influenced by Various Factors

The p-value is a crucial concept in statistical hypothesis testing, serving as a guide for making decisions about the significance of the observed relationship or effect between variables.

Let’s consider a scenario where a tutor believes that the average exam score of their students is equal to the national average (85). The tutor collects a sample of exam scores from their students and performs a one-sample t-test to compare it to the population mean (85).

• The code performs a one-sample t-test to compare the mean of a sample data set to a hypothesized population mean.
• It utilizes the scipy.stats library to calculate the t-statistic and p-value. SciPy is a Python library that provides efficient numerical routines for scientific computing.
• The p-value is compared to a significance level (alpha) to determine whether to reject the null hypothesis.

Since, 0.7059>0.05 , we would conclude to fail to reject the null hypothesis. This means that, based on the sample data, there isn’t enough evidence to claim a significant difference in the exam scores of the tutor’s students compared to the national average. The tutor would accept the null hypothesis, suggesting that the average exam score of their students is statistically consistent with the national average.

• During Forward and Backward propagation: When fitting a model (say a Multiple Linear Regression model), we use the p-value in order to find the most significant variables that contribute significantly in predicting the output.
• Effects of various drug medicines: It is highly used in the field of medical research in determining whether the constituents of any drug will have the desired effect on humans or not. P-value is a very strong statistical tool used in hypothesis testing. It provides a plethora of valuable information while making an important decision like making a business intelligence inference or determining whether a drug should be used on humans or not, etc. For any doubt/query, comment below.

The p-value is a crucial concept in statistical hypothesis testing, providing a quantitative measure of the strength of evidence against the null hypothesis. It guides decision-making by comparing the p-value to a chosen significance level, typically 0.05. A small p-value indicates strong evidence against the null hypothesis, suggesting a statistically significant relationship or effect. However, the p-value is influenced by various factors and should be interpreted alongside other considerations, such as effect size and context.

Frequently Based Questions (FAQs)

Why is p-value greater than 1.

A p-value is a probability, and probabilities must be between 0 and 1. Therefore, a p-value greater than 1 is not possible.

What does P 0.01 mean?

It means that the observed test statistic is unlikely to occur by chance if the null hypothesis is true. It represents a 1% chance of observing the test statistic or a more extreme one under the null hypothesis.

Is 0.9 a good p-value?

A good p-value is typically less than or equal to 0.05, indicating that the null hypothesis is likely false and the observed relationship or effect is statistically significant.

What is p-value in a model?

It is a measure of the statistical significance of a parameter in the model. It represents the probability of obtaining the observed value of the parameter or a more extreme one, assuming the null hypothesis is true.

Why is p-value so low?

A low p-value means that the observed test statistic is unlikely to occur by chance if the null hypothesis is true. It suggests that the observed relationship or effect is statistically significant and not due to random sampling variation.

How Can You Use P-value to Compare Two Different Results of a Hypothesis Test?

Compare p-values: Lower p-value indicates stronger evidence against null hypothesis, favoring results with smaller p-values in hypothesis testing.

Similar Reads

• Data Analysis with Python In this article, we will discuss how to do data analysis with Python. We will discuss all sorts of data analysis i.e. analyzing numerical data with NumPy, Tabular data with Pandas, data visualization Matplotlib, and Exploratory data analysis.  Data Analysis With Python Data Analysis is the technique 15+ min read

Introduction to Data Analysis

• What is Data Analysis? Data analysis is an essential aspect of modern decision-making processes across various sectors, including business, healthcare, finance, and academia. As organizations generate massive amounts of data daily, understanding how to extract meaningful insights from this data becomes crucial. In this ar 13 min read
• Data Analytics and its type Data analytics is an important field that involves the process of collecting, processing, and interpreting data to uncover insights and help in making decisions. Data analytics is the practice of examining raw data to identify trends, draw conclusions, and extract meaningful information. This involv 9 min read
• How to Install Numpy on Windows? Python NumPy is a general-purpose array processing package that provides tools for handling n-dimensional arrays. It provides various computing tools such as comprehensive mathematical functions, and linear algebra routines. NumPy provides both the flexibility of Python and the speed of well-optimiz 3 min read
• How to Install Pandas in Python? Pandas in Python is a package that is written for data analysis and manipulation. Pandas offer various operations and data structures to perform numerical data manipulations and time series. Pandas is an open-source library that is built over Numpy libraries. Pandas library is known for its high pro 5 min read
• How to Install Matplotlib on python? Matplotlib is an amazing visualization library in Python for 2D plots of arrays. Matplotlib is a multi-platform data visualization library built on NumPy arrays and designed to work with the broader SciPy stack. In this article, we will look into the various process of installing Matplotlib on Windo 2 min read
• How to Install Python Tensorflow in Windows? Tensorflow is a free and open-source software library used to do computational mathematics to build machine learning models more profoundly deep learning models. It is a product of Google built by Google’s brain team, hence it provides a vast range of operations performance with ease that is compati 3 min read

Data Analysis Libraries

• Pandas Tutorial Pandas is an open-source library that is built on top of NumPy library. Pandas is mainly popular for importing and analyzing data much easier. Pandas is a Python library for data analysis and manipulation, with high-level data structures like Series and DataFrame.Ensures compatibility with numerical 15+ min read
• NumPy Tutorial - Python Library NumPy is a general-purpose array-processing Python library which provides handy methods/functions for working n-dimensional arrays. NumPy is a short form for "Numerical Python". It provides various computing tools such as comprehensive mathematical functions, and linear algebra routines. NumPy provi 8 min read
• Data Analysis with SciPy Scipy is a Python library useful for solving many mathematical equations and algorithms. It is designed on the top of Numpy library that gives more extension of finding scientific mathematical formulae like Matrix Rank, Inverse, polynomial equations, LU Decomposition, etc. Using its high-level funct 6 min read
• Introduction to TensorFlow TensorFlow is an open-source machine learning library developed by Google. TensorFlow is used to build and train deep learning models as it facilitates the creation of computational graphs and efficient execution on various hardware platforms. The article provides an comprehensive overview of tensor 11 min read

Data Visulization Libraries

• Matplotlib Tutorial Matplotlib is easy to use and an amazing visualizing library in Python. It is built on NumPy arrays and designed to work with the broader SciPy stack and consists of several plots like line, bar, scatter, histogram, etc. In this article, you'll gain a comprehensive understanding of the diverse range 8 min read
• Python Seaborn Tutorial Seaborn is a library mostly used for statistical plotting in Python. It is built on top of Matplotlib and provides beautiful default styles and color palettes to make statistical plots more attractive. In this tutorial, we will learn about Python Seaborn from basics to advance using a huge dataset o 15+ min read
• Plotly tutorial Plotly library in Python is an open-source library that can be used for data visualization and understanding data simply and easily. Plotly supports various types of plots like line charts, scatter plots, histograms, box plots, etc. So you all must be wondering why Plotly is over other visualization 15+ min read
• Introduction to Bokeh in Python Bokeh is a Python interactive data visualization. Unlike Matplotlib and Seaborn, Bokeh renders its plots using HTML and JavaScript. It targets modern web browsers for presentation providing elegant, concise construction of novel graphics with high-performance interactivity. Features of Bokeh: Some o 1 min read

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis In this article,we will be discussing univariate, bivariate, and multivariate data and their analysis. Univariate data: Univariate data refers to a type of data in which each observation or data point corresponds to a single variable. In other words, it involves the measurement or observation of a s 5 min read
• Measures of Central Tendency in Statistics Central Tendencies in Statistics are the numerical values that are used to represent mid-value or central value a large collection of numerical data. These obtained numerical values are called central or average values in Statistics. A central or average value of any statistical data or series is th 10 min read
• Measures of Spread - Range, Variance, and Standard Deviation Collecting the data and representing it in form of tables, graphs, and other distributions is essential for us. But, it is also essential that we get a fair idea about how the data is distributed, how scattered it is, and what is the mean of the data. The measures of the mean are not enough to descr 9 min read
• Interquartile Range and Quartile Deviation using NumPy and SciPy In statistical analysis, understanding the spread or variability of a dataset is crucial for gaining insights into its distribution and characteristics. Two common measures used for quantifying this variability are the interquartile range (IQR) and quartile deviation. Quartiles Quartiles are a kind 6 min read
• Anova Formula ANOVA Test, or Analysis of Variance, is a statistical method used to test the differences between means of two or more groups. Developed by Ronald Fisher in the early 20th century, ANOVA helps determine whether there are any statistically significant differences between the means of three or more in 7 min read
• Skewness of Statistical Data Skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. In simpler terms, it indicates whether the data is concentrated more on one side of the mean compared to the other side. Why is skewness important?Understanding the skewness of dat 5 min read
• How to Calculate Skewness and Kurtosis in Python? Skewness is a statistical term and it is a way to estimate or measure the shape of a distribution. It is an important statistical methodology that is used to estimate the asymmetrical behavior rather than computing frequency distribution. Skewness can be two types: Symmetrical: A distribution can be 3 min read
• Difference Between Skewness and Kurtosis What is Skewness? Skewness is an important statistical technique that helps to determine the asymmetrical behavior of the frequency distribution, or more precisely, the lack of symmetry of tails both left and right of the frequency curve. A distribution or dataset is symmetric if it looks the same t 4 min read
• Histogram | Meaning, Example, Types and Steps to Draw What is Histogram?A histogram is a graphical representation of the frequency distribution of continuous series using rectangles. The x-axis of the graph represents the class interval, and the y-axis shows the various frequencies corresponding to different class intervals. A histogram is a two-dimens 5 min read
• Interpretations of Histogram Histograms helps visualizing and comprehending the data distribution. The article aims to provide comprehensive overview of histogram and its interpretation. What is Histogram?Histograms are graphical representations of data distributions. They consist of bars, each representing the frequency or cou 7 min read
• Box Plot Box Plot is a graphical method to visualize data distribution for gaining insights and making informed decisions. Box plot is a type of chart that depicts a group of numerical data through their quartiles. In this article, we are going to discuss components of a box plot, how to create a box plot, u 7 min read
• Quantile Quantile plots The quantile-quantile( q-q plot) plot is a graphical method for determining if a dataset follows a certain probability distribution or whether two samples of data came from the same population or not. Q-Q plots are particularly useful for assessing whether a dataset is normally distributed or if it 8 min read
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation? Data Visualisation is a graphical representation of information and data. By using different visual elements such as charts, graphs, and maps data visualization tools provide us with an accessible way to find and understand hidden trends and patterns in data. In this article, we are going to see abo 3 min read
• Using pandas crosstab to create a bar plot In this article, we will discuss how to create a bar plot by using pandas crosstab in Python. First Lets us know more about the crosstab, It is a simple cross-tabulation of two or more variables. What is cross-tabulation? It is a simple cross-tabulation that help us to understand the relationship be 3 min read
• Exploring Correlation in Python This article aims to give a better understanding of a very important technique of multivariate exploration. A correlation Matrix is basically a covariance matrix. Also known as the auto-covariance matrix, dispersion matrix, variance matrix, or variance-covariance matrix. It is a matrix in which the 4 min read
• Covariance and Correlation Covariance and correlation are the two key concepts in Statistics that help us analyze the relationship between two variables. Covariance measures how two variables change together, indicating whether they move in the same or opposite directions. In this article, we will learn about the differences 6 min read
• Factor Analysis | Data Analysis Factor analysis is a statistical method used to analyze the relationships among a set of observed variables by explaining the correlations or covariances between them in terms of a smaller number of unobserved variables called factors. Table of Content What is Factor Analysis?What does Factor mean i 13 min read
• Data Mining - Cluster Analysis INTRODUCTION: Cluster analysis, also known as clustering, is a method of data mining that groups similar data points together. The goal of cluster analysis is to divide a dataset into groups (or clusters) such that the data points within each group are more similar to each other than to data points 8 min read
• MANOVA Test in R Programming Multivariate analysis of variance (MANOVA) is simply an ANOVA (Analysis of variance) with several dependent variables. It is a continuation of the ANOVA. In an ANOVA, we test for statistical differences on one continuous dependent variable by an independent grouping variable. The MANOVA continues th 4 min read
• Python - Central Limit Theorem Central Limit Theorem (CLT) is a foundational principle in statistics, and implementing it using Python can significantly enhance data analysis capabilities. Statistics is an important part of data science projects. We use statistical tools whenever we want to make any inference about the population 7 min read
• Probability Distribution Function Probability Distribution refers to the function that gives the probability of all possible values of a random variable.It shows how the probabilities are assigned to the different possible values of the random variable.Common types of probability distributions Include: Binomial Distribution.Bernoull 9 min read
• Probability Density Estimation & Maximum Likelihood Estimation Probability density and maximum likelihood estimation (MLE) are key ideas in statistics that help us make sense of data. Probability Density Function (PDF) tells us how likely different outcomes are for a continuous variable, while Maximum Likelihood Estimation helps us find the best-fitting model f 8 min read
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions The exponential distribution in R Language is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. In R Programming Langu 2 min read
• Mathematics | Probability Distributions Set 4 (Binomial Distribution) The previous articles talked about some of the Continuous Probability Distributions. This article covers one of the distributions which are not continuous but discrete, namely the Binomial Distribution. Introduction - To understand the Binomial distribution, we must first understand what a Bernoulli 5 min read
• Poisson Distribution | Definition, Formula, Table and Examples The Poisson distribution is a type of discrete probability distribution that calculates the likelihood of a certain number of events happening in a fixed time or space, assuming the events occur independently and at a constant rate. It is characterized by a single parameter, λ (lambda), which repres 11 min read
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret A p-value is a statistical metric used to assess a hypothesis by comparing it with observed data. This article delves into the concept of p-value, its calculation, interpretation, and significance. It also explores the factors that influence p-value and highlights its limitations. Table of Content W 12 min read
• Z-Score in Statistics | Definition, Formula, Calculation and Uses Z-Score in statistics is a measurement of how many standard deviations away a data point is from the mean of a distribution. A z-score of 0 indicates that the data point's score is the same as the mean score. A positive z-score indicates that the data point is above average, while a negative z-score 15+ min read
• How to Calculate Point Estimates in R? Point estimation is a technique used to find the estimate or approximate value of population parameters from a given data sample of the population. The point estimate is calculated for the following two measuring parameters: Measuring parameterPopulation ParameterPoint EstimateProportionπp Meanμx̄ T 3 min read
• Confidence Interval In the realm of statistics, precise estimation is paramount to drawing meaningful insights from data. One of the indispensable tools in this pursuit is the confidence interval. Confidence intervals provide a systematic approach to quantifying the uncertainty associated with sample statistics, offeri 12 min read
• Chi-square test in Machine Learning Chi-Square test is a statistical method crucial for analyzing associations in categorical data. Its applications span various fields, aiding researchers in understanding relationships between factors. This article elucidates Chi-Square types, steps for implementation, and its role in feature selecti 11 min read
• Understanding Hypothesis Testing Hypothesis testing is a fundamental statistical method employed in various fields, including data science, machine learning, and statistics, to make informed decisions based on empirical evidence. It involves formulating assumptions about population parameters using sample statistics and rigorously 15+ min read

Data Preprocessing

• ML | Data Preprocessing in Python In order to derive knowledge and insights from data, the area of data science integrates statistical analysis, machine learning, and computer programming. It entails gathering, purifying, and converting unstructured data into a form that can be analysed and visualised. Data scientists process and an 7 min read
• ML | Overview of Data Cleaning Data cleaning is one of the important parts of machine learning. It plays a significant part in building a model. In this article, we'll understand Data cleaning, its significance and Python implementation. What is Data Cleaning?Data cleaning is a crucial step in the machine learning (ML) pipeline, 15 min read
• ML | Handling Missing Values Missing values are a common issue in machine learning. This occurs when a particular variable lacks data points, resulting in incomplete information and potentially harming the accuracy and dependability of your models. It is essential to address missing values efficiently to ensure strong and impar 12 min read
• Detect and Remove the Outliers using Python Outliers, deviating significantly from the norm, can distort measures of central tendency and affect statistical analyses. The piece explores common causes of outliers, from errors to intentional introduction, and highlights their relevance in outlier mining during data analysis. The article delves 10 min read

Data Transformation

• Data Normalization Machine Learning Normalization is an essential step in the preprocessing of data for machine learning models, and it is a feature scaling technique. Normalization is especially crucial for data manipulation, scaling down, or up the range of data before it is utilized for subsequent stages in the fields of soft compu 9 min read
• Sampling distribution Using Python There are different types of distributions that we study in statistics like normal/gaussian distribution, exponential distribution, binomial distribution, and many others. We will study one such distribution today which is Sampling Distribution. Let's say we have some data then if we sample some fin 3 min read

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data Data mining refers to extracting or mining knowledge from large amounts of data. In other words, Data mining is the science, art, and technology of discovering large and complex bodies of data in order to discover useful patterns. Theoreticians and practitioners are continually seeking improved tech 3 min read
• Basic DateTime Operations in Python Python has an in-built module named DateTime to deal with dates and times in numerous ways. In this article, we are going to see basic DateTime operations in Python. There are six main object classes with their respective components in the datetime module mentioned below: datetime.datedatetime.timed 12 min read
• Time Series Analysis & Visualization in Python Every dataset has distinct qualities that function as essential aspects in the field of data analytics, providing insightful information about the underlying data. Time series data is one kind of dataset that is especially important. This article delves into the complexities of time series datasets, 11 min read
• How to deal with missing values in a Timeseries in Python? It is common to come across missing values when working with real-world data. Time series data is different from traditional machine learning datasets because it is collected under varying conditions over time. As a result, different mechanisms can be responsible for missing records at different tim 10 min read
• How to calculate MOVING AVERAGE in a Pandas DataFrame? Calculating the moving average in a Pandas DataFrame is used for smoothing time series data and identifying trends. The moving average, also known as the rolling mean, helps reduce noise and highlight significant patterns by averaging data points over a specific window. In Pandas, this can be achiev 7 min read
• What is a trend in time series? Time series data is a sequence of data points that measure some variable over ordered period of time. It is the fastest-growing category of databases as it is widely used in a variety of industries to understand and forecast data patterns. So while preparing this time series data for modeling it's i 3 min read
• How to Perform an Augmented Dickey-Fuller Test in R Augmented Dickey-Fuller Test: It is a common test in statistics and is used to check whether a given time series is at rest. A given time series can be called stationary or at rest if it doesn't have any trend and depicts a constant variance over time and follows autocorrelation structure over a per 3 min read
• AutoCorrelation Autocorrelation is a fundamental concept in time series analysis. Autocorrelation is a statistical concept that assesses the degree of correlation between the values of variable at different time points. The article aims to discuss the fundamentals and working of Autocorrelation. Table of Content Wh 10 min read

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects Did you think data is only for big companies and corporations to analyze and obtain business insights? No, data is also fun! There is nothing more interesting than analyzing a data set to find the correlations between the data and obtain unique insights. It’s almost like a mystery game where the dat 7 min read
• Step by Step Predictive Analysis - Machine Learning Predictive analytics involves certain manipulations on data from existing data sets with the goal of identifying some new trends and patterns. These trends and patterns are then used to predict future outcomes and trends. By performing predictive analysis, we can predict future trends and performanc 3 min read
• 6 Tips for Creating Effective Data Visualizations The reality of things has completely changed, making data visualization a necessary aspect when you intend to make any decision that impacts your business growth. Data is no longer for data professionals; it now serves as the center of all decisions you make on your daily operations. It's vital to e 6 min read

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

P-Value And Statistical Significance: What It Is & Why It Matters

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.

Hypothesis testing

When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.

The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.

The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.

The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).

What a p-value tells you

A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).

The level of statistical significance is often expressed as a p-value between 0 and 1.

The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.

Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.

Example: Test Statistic and p-Value

Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.

P-value interpretation

The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.

This suggests the effect under study likely represents a real relationship rather than just random chance.

For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05. 

It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Therefore, we reject the null hypothesis and accept the alternative hypothesis.

Example: Statistical Significance

Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.

What does a p-value of 0.001 mean?

A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.

Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.

Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.

Note : when the p-value is above your threshold of significance,  it does not mean that there is a 95% probability that the alternative hypothesis is true.

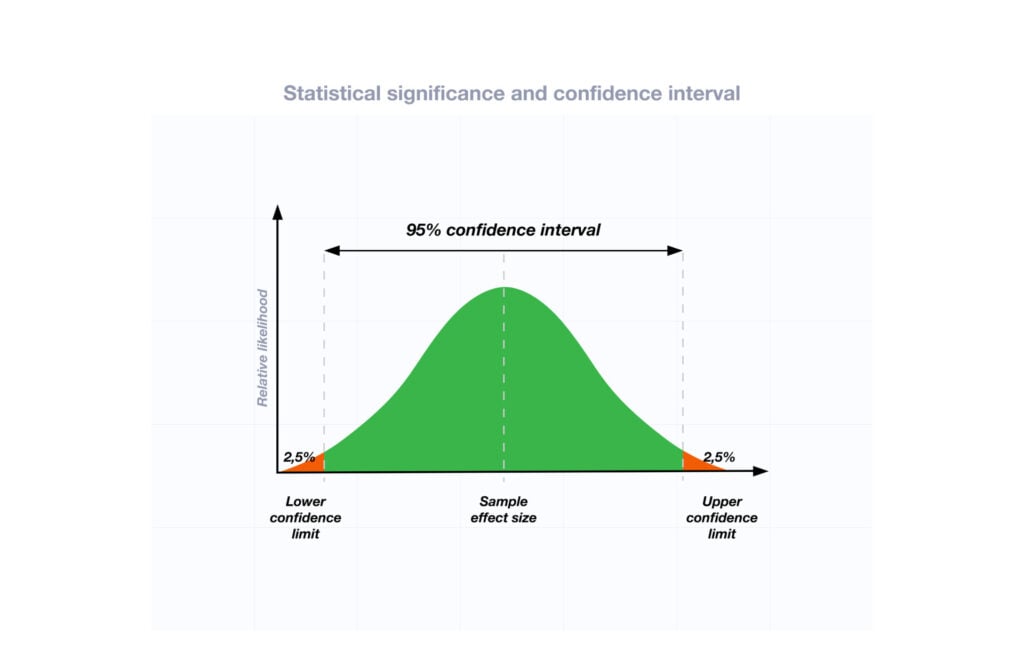
One-Tailed Test

Two-Tailed Test

How do you calculate the p-value ?

Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.

Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.

These tables help you understand how often you would expect to see your test statistic under the null hypothesis.

Understanding the Statistical Test:

Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.

For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.

Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.

This factor is particularly important to consider when comparing results across different analyses.

Example: Choosing a Statistical Test

If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.

How to report

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).

Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).

Example: Reporting the results

In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD  = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).

The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:

“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.

The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)

• Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
• Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
• p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
• The opposite of significant is “nonsignificant,” not “insignificant.”

Why is the p -value not enough?

A lower p-value  is sometimes interpreted as meaning there is a stronger relationship between two variables.

However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).

To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .

When do you reject the null hypothesis?

In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.

Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.

The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.

What does p-value of 0.05 mean?

If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.

Are all p-values below 0.05 considered statistically significant?

No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.

A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.

Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.

How does sample size affect the interpretation of p-values?

Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.

With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.

Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.

Can a non-significant p-value indicate that there is no effect or difference in the data?

No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.

There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.

Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.

Can P values be exactly zero?

While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001

Further Information

• P Value Calculator From T Score
• P-Value Calculator For Chi-Square
• P-values and significance tests (Kahn Academy)
• Hypothesis testing and p-values (Kahn Academy)
• Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
• Criticism of using the “ p “< 0.05”.
• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply.  BMJ: British Medical Journal ,  309 (6958), 874.

Goodman, S. N., & Royall, R. (1988). Evidence and scientific research.  American Journal of Public Health ,  78 (12), 1568-1574.

Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In  Seminars in hematology  (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value.  Epidemiology (Cambridge, Mass.) ,  9 (1), 7-8.

• Search Search Please fill out this field.

What Is P-Value?

What is p-value used for, how is p-value calculated.

• P-Value in Hypothesis Testing

The Bottom Line

• Corporate Finance
• Financial Analysis

P-Value: What It Is, How to Calculate It, and Examples

A p-value, or probability value, is a number describing the likelihood of obtaining the observed data under the null hypothesis of a statistical test.

The p-value serves as an alternative to rejection points to provide the smallest level of significance at which the null hypothesis would be rejected. A smaller p-value means stronger evidence in favor of the alternative hypothesis.

Key Takeaways

• A p-value is a statistical measurement used to validate a hypothesis against observed data.
• A p-value measures the probability of obtaining the observed results, assuming that the null hypothesis is true.
• The lower the p-value, the greater the statistical significance of the observed difference.
• A p-value of 0.05 or lower is generally considered statistically significant.
• P-value can serve as an alternative to—or in addition to—preselected confidence levels for hypothesis testing.

Jessica Olah / Investopedia

P-value is often used to promote credibility for studies by scientists and medical researchers as well as reports by government agencies. For example, the U.S. Census Bureau stipulates that any analysis with a p-value greater than 0.10 must be accompanied by a statement that the difference is not statistically different from zero. The Census Bureau also has standards in place stipulating which p-values are acceptable for various publications.

P-values are usually calculated using statistical software or p-value tables based on the assumed or known probability distribution of the specific statistic tested. While the sample size influences the reliability of the observed data, the p-value approach to hypothesis testing specifically involves calculating the p-value based on the deviation between the observed value and a chosen reference value, given the probability distribution of the statistic. A greater difference between the two values corresponds to a lower p-value.

Mathematically, the p-value is calculated using integral calculus from the area under the probability distribution curve for all values of statistics that are at least as far from the reference value as the observed value is, relative to the total area under the probability distribution curve. Standard deviations, which quantify the dispersion of data points from the mean, are instrumental in this calculation.

The calculation for a p-value varies based on the type of test performed. The three test types describe the location on the probability distribution curve: lower-tailed test, upper-tailed test, or two-tailed test . In each case, the degrees of freedom play a crucial role in determining the shape of the distribution and thus, the calculation of the p-value.

In a nutshell, the greater the difference between two observed values, the less likely it is that the difference is due to simple random chance, and this is reflected by a lower p-value.

What Is the Significance of a P-Value?

The p-value approach to hypothesis testing uses the calculated probability to determine whether there is evidence to reject the null hypothesis. This determination relies heavily on the test statistic, which summarizes the information from the sample relevant to the hypothesis being tested. The null hypothesis, also known as the conjecture, is the initial claim about a population (or data-generating process). The alternative hypothesis states whether the population parameter differs from the value of the population parameter stated in the conjecture.

In practice, the significance level is stated in advance to determine how small the p-value must be to reject the null hypothesis. Because different researchers use different levels of significance when examining a question, a reader may sometimes have difficulty comparing results from two different tests. P-values provide a solution to this problem.

How to interpret p-value: Even a low p-value is not necessarily proof of statistical significance, since there is still a possibility that the observed data are the result of chance. Only repeated experiments or studies can confirm if a relationship is statistically significant.

For example, suppose a study comparing returns from two particular assets was undertaken by different researchers who used the same data but different significance levels. The researchers might come to opposite conclusions regarding whether the assets differ.

If one researcher used a confidence level of 90% and the other required a confidence level of 95% to reject the null hypothesis, and if the p-value of the observed difference between the two returns was 0.08 (corresponding to a confidence level of 92%), then the first researcher would find that the two assets have a difference that is statistically significant , while the second would find no statistically significant difference between the returns.

To avoid this problem, the researchers could report the p-value of the hypothesis test and allow readers to interpret the statistical significance themselves. This is called a p-value approach to hypothesis testing. Independent observers could note the p-value and decide for themselves whether that represents a statistically significant difference or not.

Example of P-Value

An investor claims that their investment portfolio’s performance is equivalent to that of the Standard & Poor’s (S&P) 500 Index . To determine this, the investor conducts a two-tailed test.

The null hypothesis states that the portfolio’s returns are equivalent to the S&P 500’s returns over a specified period, while the alternative hypothesis states that the portfolio’s returns and the S&P 500’s returns are not equivalent—if the investor conducted a one-tailed test , the alternative hypothesis would state that the portfolio’s returns are either less than or greater than the S&P 500’s returns.

The p-value hypothesis test does not necessarily make use of a preselected confidence level at which the investor should reset the null hypothesis that the returns are equivalent. Instead, it provides a measure of how much evidence there is to reject the null hypothesis. The smaller the p-value, the greater the evidence against the null hypothesis.

Thus, if the investor finds that the p-value is 0.001, there is strong evidence against the null hypothesis, and the investor can confidently conclude that the portfolio’s returns and the S&P 500’s returns are not equivalent.

Although this does not provide an exact threshold as to when the investor should accept or reject the null hypothesis, it does have another very practical advantage. P-value hypothesis testing offers a direct way to compare the relative confidence that the investor can have when choosing among multiple different types of investments or portfolios relative to a benchmark such as the S&P 500.

For example, for two portfolios, A and B, whose performance differs from the S&P 500 with p-values of 0.10 and 0.01, respectively, the investor can be much more confident that portfolio B, with a lower p-value, will actually show consistently different results.

Is a 0.05 P-Value Significant?

A p-value less than 0.05 is typically considered to be statistically significant, in which case the null hypothesis should be rejected. A p-value greater than 0.05 means that deviation from the null hypothesis is not statistically significant, and the null hypothesis is not rejected.

What Does a P-Value of 0.001 Mean?

A p-value of 0.001 indicates that if the null hypothesis tested were indeed true, then there would be a one-in-1,000 chance of observing results at least as extreme. This leads the observer to reject the null hypothesis because either a highly rare data result has been observed or the null hypothesis is incorrect.

How Can You Use P-Value to Compare Two Different Results of a Hypothesis Test?

If you have two different results, one with a p-value of 0.04 and one with a p-value of 0.06, the result with a p-value of 0.04 will be considered more statistically significant than the p-value of 0.06. Beyond this simplified example, you could compare a 0.04 p-value to a 0.001 p-value. Both are statistically significant, but the 0.001 example provides an even stronger case against the null hypothesis than the 0.04.

The p-value is used to measure the significance of observational data. When researchers identify an apparent relationship between two variables, there is always a possibility that this correlation might be a coincidence. A p-value calculation helps determine if the observed relationship could arise as a result of chance.

U.S. Census Bureau. “ Statistical Quality Standard E1: Analyzing Data .”

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

An Explanation of P-Values and Statistical Significance

In statistics, p-values are commonly used in hypothesis testing for t-tests, chi-square tests, regression analysis, ANOVAs, and a variety of other statistical methods.

Despite being so common, people often interpret p-values incorrectly, which can lead to errors when interpreting the findings from an analysis or a study. 

This post explains how to understand and interpret p-values in a clear, practical way.

Hypothesis Testing

To understand p-values, we first need to understand the concept of hypothesis testing .

A  hypothesis test  is a formal statistical test we use to reject or fail to reject some hypothesis. For example, we may hypothesize that a new drug, method, or procedure provides some benefit over a current drug, method, or procedure. 

To test this, we can conduct a hypothesis test where we use a null and alternative hypothesis:

Null hypothesis – There is no effect or difference between the new method and the old method.

Alternative hypothesis – There does exist some effect or difference between the new method and the old method.

A p-value indicates how believable the null hypothesis is, given the sample data. Specifically, assuming the null hypothesis is true, the p-value tells us the probability of obtaining an effect at least as large as the one we actually observed in the sample data. 

If the p-value of a hypothesis test is sufficiently low, we can reject the null hypothesis. Specifically, when we conduct a hypothesis test, we must choose a significance level at the outset. Common choices for significance levels are 0.01, 0.05, and 0.10.

If the p-values is  less than  our significance level, then we can reject the null hypothesis.

Otherwise, if the p-value is  equal to or greater than  our significance level, then we fail to reject the null hypothesis. 

How to Interpret a P-Value

The textbook definition of a p-value is:

A p-value is the probability of observing a sample statistic that is at least as extreme as your sample statistic, given that the null hypothesis is true.

For example, suppose a factory claims that they produce tires that have a mean weight of 200 pounds. An auditor hypothesizes that the true mean weight of tires produced at this factory is different from 200 pounds so he runs a hypothesis test and finds that the p-value of the test is 0.04. Here is how to interpret this p-value:

If the factory does indeed produce tires that have a mean weight of 200 pounds, then 4% of all audits will obtain the effect observed in the sample, or larger, because of random sample error. This tells us that obtaining the sample data that the auditor did would be pretty rare if indeed the factory produced tires that have a mean weight of 200 pounds. 

Depending on the significance level used in this hypothesis test, the auditor would likely reject the null hypothesis that the true mean weight of tires produced at this factory is indeed 200 pounds. The sample data that he obtained from the audit is not very consistent with the null hypothesis.

How Not  to Interpret a P-Value

The biggest misconception about p-values is that they are equivalent to the probability of making a mistake by rejecting a true null hypothesis (known as a Type I error).

There are two primary reasons that p-values can’t be the error rate:

1.  P-values are calculated based on the assumption that the null hypothesis is true and that the difference between the sample data and the null hypothesis is simple caused by random chance. Thus, p-values can’t tell you the probability that the null is true or false since it is 100% true based on the perspective of the calculations.

2. Although a low p-value indicates that your sample data are unlikely assuming the null is true, a p-value still can’t tell you which of the following cases is more likely:

• The null is false
• The null is true but you obtained an odd sample

In regards to the previous example, here is a correct and incorrect way to interpret the p-value:

• Correct Interpretation: Assuming the factory does produce tires with a mean weight of 200 pounds, you would obtain the observed difference that you  did  obtain in your sample or a more extreme difference in 4% of audits due to random sampling error.
• Incorrect Interpretation: If you reject the null hypothesis, there is a 4% chance that you are making a mistake.

Examples of Interpreting P-Values

The following examples illustrate correct ways to interpret p-values in the context of hypothesis testing.

A phone company claims that 90% of its customers are satisfied with their service. To test this claim, an independent researcher gathered a simple random sample of 200 customers and asked them if they are satisfied with their service, to which 85% responded yes. The p-value associated with this sample data turned out to be 0.018.

Correct interpretation of p-value:  Assuming that 90% of the customers actually are satisfied with their service, the researcher would obtain the observed difference that he  did  obtain in his sample or a more extreme difference in 1.8% of audits due to random sampling error.

A company invents a new battery for phones. The company claims that this new battery will work for at least 10 minutes longer than the old battery. To test this claim, a researcher takes a simple random sample of 80 new batteries and 80 old batteries. The new batteries run for an average of 120 minutes with a standard deviation of 12 minutes and the old batteries run for an average of 115 minutes with a standard deviation of 15 minutes. The p-value that results from the test for a difference in population means is 0.011.

Correct interpretation of p-value:  Assuming that the new battery works for the same amount of time or less than the old battery, the researcher would obtain the observed difference or a more extreme difference in 1.1% of studies due to random sampling error.

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “An Explanation of P-Values and Statistical Significance”

My concepts are actually getting clear because of the consice and simple way, with ample examples. Thank you statology!

I read this article and its written amazingly in a simplified way.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

9.3 - the p-value approach, example 9-4 section  .

Up until now, we have used the critical region approach in conducting our hypothesis tests. Now, let's take a look at an example in which we use what is called the P -value approach .

Among patients with lung cancer, usually, 90% or more die within three years. As a result of new forms of treatment, it is felt that this rate has been reduced. In a recent study of n = 150 lung cancer patients, y = 128 died within three years. Is there sufficient evidence at the \(\alpha = 0.05\) level, say, to conclude that the death rate due to lung cancer has been reduced?

The sample proportion is:

\(\hat{p}=\dfrac{128}{150}=0.853\)

The null and alternative hypotheses are:

\(H_0 \colon p = 0.90\) and \(H_A \colon p < 0.90\)

The test statistic is, therefore:

\(Z=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{p_0(1-p_0)}{n}}}=\dfrac{0.853-0.90}{\sqrt{\dfrac{0.90(0.10)}{150}}}=-1.92\)

And, the rejection region is:

Since the test statistic Z = −1.92 < −1.645, we reject the null hypothesis. There is sufficient evidence at the \(\alpha = 0.05\) level to conclude that the rate has been reduced.

Example 9-4 (continued) Section  

What if we set the significance level \(\alpha\) = P (Type I Error) to 0.01? Is there still sufficient evidence to conclude that the death rate due to lung cancer has been reduced?

In this case, with \(\alpha = 0.01\), the rejection region is Z ≤ −2.33. That is, we reject if the test statistic falls in the rejection region defined by Z ≤ −2.33:

Because the test statistic Z = −1.92 > −2.33, we do not reject the null hypothesis. There is insufficient evidence at the \(\alpha = 0.01\) level to conclude that the rate has been reduced.

In the first part of this example, we rejected the null hypothesis when \(\alpha = 0.05\). And, in the second part of this example, we failed to reject the null hypothesis when \(\alpha = 0.01\). There must be some level of \(\alpha\), then, in which we cross the threshold from rejecting to not rejecting the null hypothesis. What is the smallest \(\alpha \text{ -level}\) that would still cause us to reject the null hypothesis?

We would, of course, reject any time the critical value was smaller than our test statistic −1.92:

That is, we would reject if the critical value were −1.645, −1.83, and −1.92. But, we wouldn't reject if the critical value were −1.93. The \(\alpha \text{ -level}\) associated with the test statistic −1.92 is called the P -value . It is the smallest \(\alpha \text{ -level}\) that would lead to rejection. In this case, the P -value is:

P ( Z < −1.92) = 0.0274

So far, all of the examples we've considered have involved a one-tailed hypothesis test in which the alternative hypothesis involved either a less than (<) or a greater than (>) sign. What happens if we weren't sure of the direction in which the proportion could deviate from the hypothesized null value? That is, what if the alternative hypothesis involved a not-equal sign (≠)? Let's take a look at an example.

What if we wanted to perform a " two-tailed " test? That is, what if we wanted to test:

\(H_0 \colon p = 0.90\) versus \(H_A \colon p \ne 0.90\)

at the \(\alpha = 0.05\) level?

Let's first consider the critical value approach . If we allow for the possibility that the sample proportion could either prove to be too large or too small, then we need to specify a threshold value, that is, a critical value, in each tail of the distribution. In this case, we divide the " significance level " \(\alpha\) by 2 to get \(\alpha/2\):

That is, our rejection rule is that we should reject the null hypothesis \(H_0 \text{ if } Z ≥ 1.96\) or we should reject the null hypothesis \(H_0 \text{ if } Z ≤ −1.96\). Alternatively, we can write that we should reject the null hypothesis \(H_0 \text{ if } |Z| ≥ 1.96\). Because our test statistic is −1.92, we just barely fail to reject the null hypothesis, because 1.92 < 1.96. In this case, we would say that there is insufficient evidence at the \(\alpha = 0.05\) level to conclude that the sample proportion differs significantly from 0.90.

Now for the P -value approach . Again, needing to allow for the possibility that the sample proportion is either too large or too small, we multiply the P -value we obtain for the one-tailed test by 2:

That is, the P -value is:

\(P=P(|Z|\geq 1.92)=P(Z>1.92 \text{ or } Z<-1.92)=2 \times 0.0274=0.055\)

Because the P -value 0.055 is (just barely) greater than the significance level \(\alpha = 0.05\), we barely fail to reject the null hypothesis. Again, we would say that there is insufficient evidence at the \(\alpha = 0.05\) level to conclude that the sample proportion differs significantly from 0.90.

Let's close this example by formalizing the definition of a P -value, as well as summarizing the P -value approach to conducting a hypothesis test.

The P -value is the smallest significance level \(\alpha\) that leads us to reject the null hypothesis.

Alternatively (and the way I prefer to think of P -values), the P -value is the probability that we'd observe a more extreme statistic than we did if the null hypothesis were true.

If the P -value is small, that is, if \(P ≤ \alpha\), then we reject the null hypothesis \(H_0\).

Note! Section  

By the way, to test \(H_0 \colon p = p_0\), some statisticians will use the test statistic:

\(Z=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}}\)

rather than the one we've been using:

\(Z=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{p_0(1-p_0)}{n}}}\)

One advantage of doing so is that the interpretation of the confidence interval — does it contain \(p_0\)? — is always consistent with the hypothesis test decision, as illustrated here:

For the sake of ease, let:

\(se(\hat{p})=\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)

Two-tailed test. In this case, the critical region approach tells us to reject the null hypothesis \(H_0 \colon p = p_0\) against the alternative hypothesis \(H_A \colon p \ne p_0\):

if \(Z=\dfrac{\hat{p}-p_0}{se(\hat{p})} \geq z_{\alpha/2}\) or if \(Z=\dfrac{\hat{p}-p_0}{se(\hat{p})} \leq -z_{\alpha/2}\)

which is equivalent to rejecting the null hypothesis:

if \(\hat{p}-p_0 \geq z_{\alpha/2}se(\hat{p})\) or if \(\hat{p}-p_0 \leq -z_{\alpha/2}se(\hat{p})\)

if \(p_0 \geq \hat{p}+z_{\alpha/2}se(\hat{p})\) or if \(p_0 \leq \hat{p}-z_{\alpha/2}se(\hat{p})\)

That's the same as saying that we should reject the null hypothesis \(H_0 \text{ if } p_0\) is not in the \(\left(1-\alpha\right)100\%\) confidence interval!

Left-tailed test. In this case, the critical region approach tells us to reject the null hypothesis \(H_0 \colon p = p_0\) against the alternative hypothesis \(H_A \colon p < p_0\):

if \(Z=\dfrac{\hat{p}-p_0}{se(\hat{p})} \leq -z_{\alpha}\)

if \(\hat{p}-p_0 \leq -z_{\alpha}se(\hat{p})\)

if \(p_0 \geq \hat{p}+z_{\alpha}se(\hat{p})\)

That's the same as saying that we should reject the null hypothesis \(H_0 \text{ if } p_0\) is not in the upper \(\left(1-\alpha\right)100\%\) confidence interval:

\((0,\hat{p}+z_{\alpha}se(\hat{p}))\)