statistical significance research

• Sign Up Now
• -- Navigate To -- CR Dashboard Connect for Researchers Connect for Participants
• Log In Log Out Log In
• Recent Press
• Papers Citing Connect
• Connect for Participants
• Connect for Researchers
• Connect AI Training
• Managed Research
• Prime Panels
• MTurk Toolkit
• Health & Medicine
• Enterprise Accounts
• Conferences
• Knowledge Base
• A Researcher’s Guide To Statistical Significance And Sample Size Calculations

What Does It Mean for Research to Be Statistically Significant?

Quick Navigation:

What does it mean to be statistically significant, an example of null hypothesis significance testing, measuring statistical significance: understanding the p value (significance level), what factors affect the power of hypothesis test, 1. sample size, 2. significance level, 3. standard deviations, 4. effect size, why is statistical significance important for researchers, does your study need to be statistically significant, practical significance vs. statistical significance, part 1: how is statistical significance defined in research.

The world today is drowning in data.

That may sound like hyperbole but consider this. In 2018, humans around the world produced more than 2.5 quintillion bytes of data—each day. According to some estimates , every minute people conduct almost 4.5 million Google searches, post 511,200 tweets, watch 4.5 million YouTube videos, swipe 1.4 million times on Tinder, and order 8,683 meals from GrubHub. These numbers—and the world’s total data—are expected to continue growing exponentially in the coming years.

For behavioral researchers and businesses, this data represents a valuable opportunity. However, using data to learn about human behavior or make decisions about consumer behavior often requires an understanding of statistics and statistical significance.

Statistical significance is a measurement of how likely it is that the difference between two groups, models, or statistics occurred by chance or occurred because two variables are actually related to each other. This means that a “statistically significant” finding is one in which it is likely the finding is real, reliable, and not due to chance.

To evaluate whether a finding is statistically significant, researchers engage in a process known as null hypothesis significance testing . Null hypothesis significance testing is less of a mathematical formula and more of a logical process for thinking about the strength and legitimacy of a finding.

Imagine a Vice President of Marketing asks her team to test a new layout for the company website. The new layout streamlines the user experience by making it easier for people to place orders and suggesting additional items to go along with each customer’s purchase. After testing the new website, the VP finds that visitors to the site spend an average of $12.63. Under the old layout, visitors spent an average of $12.32, meaning the new layout increases average spending by $0.31 per person. The question the VP must answer is whether the difference of $0.31 per person is significant or something that likely occurred by chance.

To answer this question with statistical analysis, the VP begins by adopting a skeptical stance toward her data known as the null hypothesis . The null hypothesis assumes that whatever researchers are studying does not actually exist in the population of interest. So, in this case the VP assumes that the change in website layout does not influence how much people spend on purchases.

With the null hypothesis in mind, the manager asks how likely it is that she would obtain the results observed in her study—the average difference of $0.31 per visitor—if the change in website layout actually causes no difference in people’s spending (i.e., if the null hypothesis is true). If the probability of obtaining the observed results is low, the manager will reject the null hypothesis and conclude that her finding is statistically significant.

Statistically significant findings indicate not only that the researchers’ results are unlikely the result of chance, but also that there is an effect or relationship between the variables being studied in the larger population. However, because researchers want to ensure they do not falsely conclude there is a meaningful difference between groups when in fact the difference is due to chance, they often set stringent criteria for their statistical tests. This criterion is known as the significance level .

Within the social sciences, researchers often adopt a significance level of 5%. This means researchers are only willing to conclude that the results of their study are statistically significant if the probability of obtaining those results if the null hypothesis were true—known as the p value —is less than 5%.

Five percent represents a stringent criterion, but there is nothing magical about it. In medical research, significance levels are often set at 1%. In cognitive neuroscience, researchers often adopt significance levels well below 1%. And, when astronomers seek to explain aspects of the universe or physicists study new particles like the Higgs Boson they set significance levels several orders of magnitude below .05.

In other research contexts like business or industry, researchers may set more lenient significance levels depending on the aim of their research. However, in all research, the more stringently a researcher sets their significance level, the more confident they can be that their results are not due to chance.

Determining whether a given set of results is statistically significant is only one half of the hypothesis testing equation. The other half is ensuring that the statistical tests a researcher conducts are powerful enough to detect an effect if one really exists. That is, when a researcher concludes their hypothesis was incorrect and there is no effect between the variables being studied, that conclusion is only meaningful if the study was powerful enough to detect an effect if one really existed.

The power of a hypothesis test is influenced by several factors.

Sample size—or, the number of participants the researcher collects data from—affects the power of a hypothesis test. Larger samples with more observations generally lead to higher-powered tests than smaller samples. In addition, large samples are more likely to produce replicable results because extreme scores that occur by chance are more likely to balance out in a large sample rather than in a small one.

Although setting a low significance level helps researchers ensure their results are not due to chance, it also lowers their power to detect an effect because it makes rejecting the null hypothesis harder. In this respect, the significance level a researcher selects is often in competition with power.

Standard deviations represent unexplained variability within data, also known as error. Generally speaking, the more unexplained variability within a dataset, the less power researchers have to detect an effect. Unexplained variability can be the result of measurement error, individual differences among participants, or situational noise.   

A final factor that influences power is the size of the effect a researcher is studying. As you might expect, big changes in behavior are easier to detect than small ones.

Sometimes researchers do not know the strength of an effect before conducting a study. Even though this makes it harder to conduct a well powered study, it is important to keep in mind that phenomena that produce a large effect will lead to studies with more power than phenomena that produce only a small effect.

Statistical significance is important because it allows researchers to hold a degree of confidence that their findings are real, reliable, and not due to chance. But statistical significance is not equally important to all researchers in all situations. The importance of obtaining statistically significant results depends on what a researcher studies and within what context.

Within academic research, statistical significance is often critical because academic researchers study theoretical relationships between different variables and behavior. Furthermore, the goal of academic research is often to publish research reports in scientific journals. The threshold for publishing in academic journals is often a series of statistically significant results.

Outside of academia, statistical significance is often less important. Researchers, managers, and decision makers in business may use statistical significance to understand how strongly the results of a study should inform the decisions they make. But, because statistical significance is simply a way of quantifying how much confidence to hold in a research finding, people in industry are often more interested in a finding’s practical significance than statistical significance.

To demonstrate the difference between practical and statistical significance, imagine you’re a candidate for political office. Maybe you have decided to run for local or state-wide office, or, if you’re feeling bold, imagine you’re running for President.

During your campaign, your team comes to you with data on messages intended to mobilize voters. These messages have been market tested and now you and your team must decide which ones to adopt.

If you go with Message A, 41% of registered voters say they are likely to turn out at the polls and cast a ballot. If you go with Message B, this number drops to 37%. As a candidate, should you care whether this difference is statistically significant at a p value below .05?

The answer is of course not. What you likely care about more than statistical significance is practical significance —the likelihood that the difference between groups is large enough to be meaningful in real life.  

You should ensure there is some rigor behind the difference in messages before you spend money on a marketing campaign, but when elections are sometimes decided by as little as one vote you should adopt the message that brings more people out to vote. Within business and industry, the practical significance of a research finding is often equally if not more important than the statistical significance. In addition, when findings have large practical significance, they are almost always statistically significant too.

Conducting statistically significant research is a challenge, but it’s a challenge worth tackling. Flawed data and faulty analyses only lead to poor decisions. Start taking steps to ensure your surveys and experiments produce valid results by using CloudResearch. If you have the team to conduct your own studies, CloudResearch can help you find large samples of online participants quickly and easily. Regardless of your demographic criteria or sample size, we can help you get the participants you need. If your team doesn’t have the resources to run a study, we can run it for you. Our team of expert social scientists, computer scientists, and software engineers can design any study, collect the data, and analyze the results for you. Let us show you how conducting statistically significant research can improve your decision-making today.

Continue Reading: A Researcher’s Guide to Statistical Significance and Sample Size Calculations

Part 2: How to Calculate Statistical Significance

Part 3: Determining Sample Size: How Many Survey Participants Do You Need?

Related articles, what is data quality and why is it important.

If you were a researcher studying human behavior 30 years ago, your options for identifying participants for your studies were limited. If you worked at a university, you might be...

How to Identify and Handle Invalid Responses to Online Surveys

As a researcher, you are aware that planning studies, designing materials and collecting data each take a lot of work. So when you get your hands on a new dataset,...

SUBSCRIBE TO RECEIVE UPDATES

• Name * First name Last name
• I would like to request a demo of the Engage platform
• Email This field is for validation purposes and should be left unchanged.

2024 Grant Application Form

Personal and institutional information.

• Full Name * First Last
• Position/Title *
• Affiliated Academic Institution or Research Organization *

Detailed Research Proposal Questions

• Project Title *
• Research Category * - Antisemitism Islamophobia Both
• Objectives *
• Methodology (including who the targeted participants are) *
• Expected Outcomes *
• Significance of the Study *

Budget and Grant Tier Request

• Requested Grant Tier * - $200 $500 $1000 Applicants requesting larger grants may still be eligible for smaller awards if the full amount requested is not granted.
• Budget Justification *

Research Timeline

• Projected Start Date * MM slash DD slash YYYY Preference will be given to projects that can commence soon, preferably before September 2024.
• Estimated Completion Date * MM slash DD slash YYYY Preference will be given to projects that aim to complete within a year.
• Project Timeline *
• Comments This field is for validation purposes and should be left unchanged.

• Name * First Name Last Name
• I would like to request a demo of the Sentry platform
• Name This field is for validation purposes and should be left unchanged.

• Name * First Last
• Name * First and Last
• Please select the best time to discuss your project goals/details to claim your free Sentry pilot for the next 60 days or to receive 10% off your first Managed Research study with Sentry.

• Email * Enter Email Confirm Email
• Organization
• Job Title *
• Phone This field is for validation purposes and should be left unchanged.

P-Value And Statistical Significance: What It Is & Why It Matters

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.

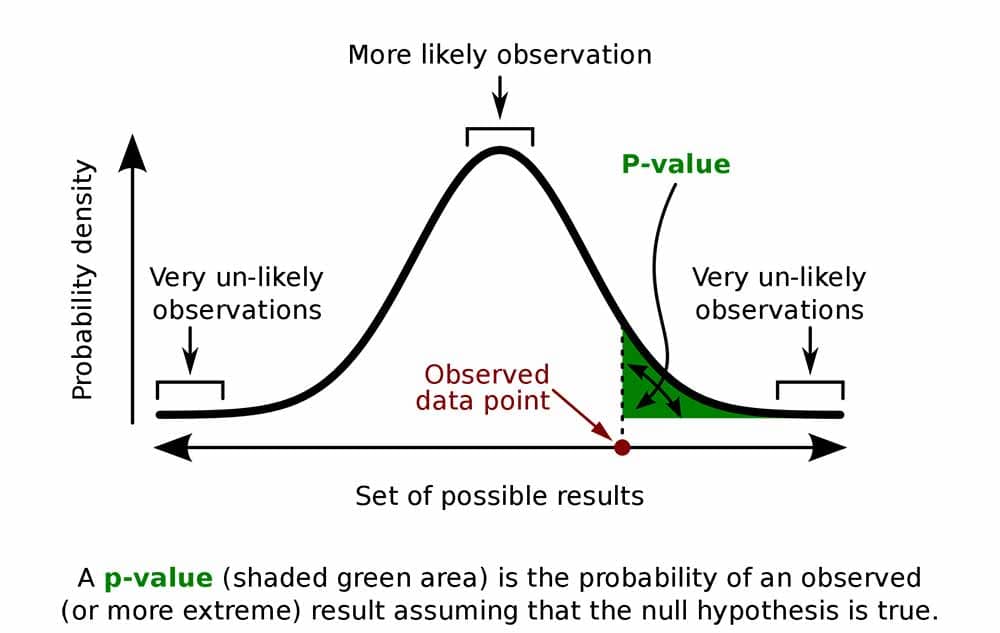
Hypothesis testing

When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.

The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.

The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.

The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).

What a p-value tells you

A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).

The level of statistical significance is often expressed as a p-value between 0 and 1.

The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.

Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.

Example: Test Statistic and p-Value

Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.

P-value interpretation

The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.

This suggests the effect under study likely represents a real relationship rather than just random chance.

For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05. 

It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Therefore, we reject the null hypothesis and accept the alternative hypothesis.

Example: Statistical Significance

Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.

What does a p-value of 0.001 mean?

A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.

Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.

Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.

Note : when the p-value is above your threshold of significance,  it does not mean that there is a 95% probability that the alternative hypothesis is true.

One-Tailed Test

Two-Tailed Test

How do you calculate the p-value ?

Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.

Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.

These tables help you understand how often you would expect to see your test statistic under the null hypothesis.

Understanding the Statistical Test:

Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.

For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.

Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.

This factor is particularly important to consider when comparing results across different analyses.

Example: Choosing a Statistical Test

If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.

How to report

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).

Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).

Example: Reporting the results

In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD  = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).

The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:

“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.

The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)

• Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
• Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
• p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
• The opposite of significant is “nonsignificant,” not “insignificant.”

Why is the p -value not enough?

A lower p-value  is sometimes interpreted as meaning there is a stronger relationship between two variables.

However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).

To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .

When do you reject the null hypothesis?

In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.

Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.

The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.

What does p-value of 0.05 mean?

If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.

Are all p-values below 0.05 considered statistically significant?

No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.

A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.

Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.

How does sample size affect the interpretation of p-values?

Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.

With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.

Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.

Can a non-significant p-value indicate that there is no effect or difference in the data?

No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.

There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.

Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.

Can P values be exactly zero?

While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001

Further Information

• P Value Calculator From T Score
• P-Value Calculator For Chi-Square
• P-values and significance tests (Kahn Academy)
• Hypothesis testing and p-values (Kahn Academy)
• Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
• Criticism of using the “ p “< 0.05”.
• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply.  BMJ: British Medical Journal ,  309 (6958), 874.

Goodman, S. N., & Royall, R. (1988). Evidence and scientific research.  American Journal of Public Health ,  78 (12), 1568-1574.

Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In  Seminars in hematology  (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value.  Epidemiology (Cambridge, Mass.) ,  9 (1), 7-8.

If you could change one thing about college, what would it be?

Graduate faster

Better quality online classes

Flexible schedule

Access to top-rated instructors

What Is Statistical Significance & Why Learn It

08.04.2023 • 6 min read

Sarah Thomas

Subject Matter Expert

Learn what statistical significance means, why it is important, and how it’s calculated, and what the levels of significance mean.

In This Article

What Is Statistical Significance?

Examples of statistical significance, how is statistical significance calculated, what does the significance level mean.

A study claims people who practice intermittent fasting experience less severe complications from COVID-19, but how seriously should you take this claim? Statistical significance is a powerful tool that can help answer this question. It’s one of the main tools we have for assessing the validity of statistical findings.

In this article, we'll dive into what statistical significance is, how it's calculated, and why it's essential for making informed decisions based on data.

Statistical significance is a core concept in statistics. We use it in hypothesis testing to determine whether the results we obtain occurred by chance or whether they point to something relevant and true about the population we are studying.

Suppose you observe dogs whose owners spend more time with them at home live longer than those whose owners spend less time with them. The basic idea behind statistical significance is this: it helps you determine whether your observation is simply due to random variation in your samples or whether there’s strong enough evidence to support an underlying difference between dogs who spend more time with their owners and those who spend less.

If your results are “statistically significant,” your observation points to a meaningful difference rather than a difference observed by chance. If your results are not statistically significant, you do not have enough statistical evidence to rule out the possibility that what you observed is due to random variation in your samples. Maybe you observed longer life spans in one group of dogs simply because you happened to sample some ‌healthy dogs in one group or some less healthy ones in the other.

Statistical significance is crucial to ensure ‌our statistical findings are trustworthy and reliable, and we use it to avoid drawing false conclusions.

We use statistical analysis in many fields, so you’ll see mentions of statistical significance in many different contexts.

Here are some examples you might come across in the real world:

In finance, you may be interested in comparing the performance of different investment portfolios. If one portfolio performs better than another, you, as an investor, could use statistical tests to see if the higher returns are statistically significant. In other words, you could test to see whether the higher returns were likely the result of random variation or whether some other reason explains why one portfolio performed better.


In medical research, you may be interested in comparing the outcomes of patients in a treatment group to those in a control group. The patients in the treatment group receive a newly developed drug to manage a disease, while patients in the treatment group do not receive the new treatment.

At the end of your study, you compare the health outcomes of each group. If you observe that the patients in the treatment group had better outcomes, you will want to conduct a hypothesis test to see if the difference in outcomes is statistically significant—i.e., due to the difference in treatment.

Agriculture

Agronomists use hypothesis tests to determine what soil conditions and management types lead to the best crop yields. Like a medical researcher who compares treatment and control groups, agronomists conduct hypothesis tests to see if there are statistically significant differences between crops grown under different conditions.

In business, there are many applications of statistical testing. For example, if you hypothesize that a product tweak led to greater customer retention, you could use a statistical test to see if your results are statistically significant.

To determine statistical significance, you first need to articulate the main elements of your hypothesis test. You’ll need to articulate a null hypothesis and an alternative hypothesis , and you’ll need to choose a significance level for your test.

The null hypothesis represents the assumption that there's no significant difference between the variables you are studying. For example, a new drug has no effect on patient outcomes.

The alternative hypothesis represents what you suspect might be true. For example, a new drug improves patient outcomes. The null and alternative hypotheses must be mutually exclusive statements, meaning that the null hypothesis must be false for the alternative hypothesis to be true.

The significance level of a hypothesis test is the threshold you use to determine whether or not your results are statistically significant. The significance level is the probability of falsely rejecting the null hypothesis when it is actually true.

The most commonly used significance levels are:

0.10 (or 10%)

0.05 (or 5%)

Once you’ve stated your hypotheses and significance level, you’ll collect data and calculate a test statistic from your data. You then need to calculate a p-value for your test statistic. A p-value represents the probability of observing a result as extreme or more extreme than the one you obtained, assuming that the null hypothesis is true.

If the p-value is smaller than your significance level, you reject the null hypothesis in favor of the alternative hypothesis. The smaller your p-value is, the more conviction you can have in rejecting the null hypothesis. If the p-value exceeds the significance level, you fail to reject the null hypothesis.

The significance level—or alpha level (α)—is a benchmark we use in statistical hypothesis testing. It is the probability threshold below which you reject the null hypothesis.

The most commonly used significance level is 0.05 (or 5%), but you can choose a lower or higher significance level in your testing depending on your priorities. With a smaller alpha, you have a smaller chance of making a Type I error in your analysis.

A Type I error is when you accidentally reject the null hypothesis when, in fact, the null hypothesis is true. On the other hand, the smaller your significance level is, the more likely you are to make a Type II error. A Type II error is when you fail to reject a false null hypothesis.

A significance level of 0.05 means if you calculate a p-value less than 0.05, you will reject the null hypothesis in favor of the alternative hypothesis. It also means you will have a 5% chance of rejecting the null hypothesis when it is actually true (i.e., you will have a 5% chance of making a Type I error).

Is statistical significance the only way to assess the validity of a statistical study?

Statistical significance is one of many things you should check for when assessing a statistical study. A statistically significant result is not enough to guarantee the validity of a statistical result. Several other factors affect the reliability of research findings, such as sample size, the type of data used, study design, and the presence of confounding variables.

You always need to use statistical significance as a tool in combination with other methods to ensure the quality of your research.

Is statistical significance the same thing as effect size?

Statistical significance and effect size are not the same thing. Statistical significance assesses whether our findings are due to random chance. Effect size measures the magnitude of the difference between two groups or the strength of the relationship between two variables.

Just because your data analysis returns statistically significant results, it does mean that you have found a large effect size. For example, you may find a statistically significant result that dogs who spend more time with their owners live longer, but you might only find a small effect.

Effect size is sometimes called practical significance because statistically significant results are only “practically significant” when the results are large enough for us to care about.

What is the difference between statistical significance and statistical power?

Statistical power is the power of a statistical test to correctly reject the null hypothesis when a given alternative hypothesis is true. It is the ability to detect an effect in a sample data set when the effect is, in fact, present in the population. Statistical significance is one of the factors that impacts power.

A higher significance level, having a larger sample, a larger effect size, and lower variability within the population, are all elements that increase statistical power.

What is the relationship between significance levels and confidence levels?

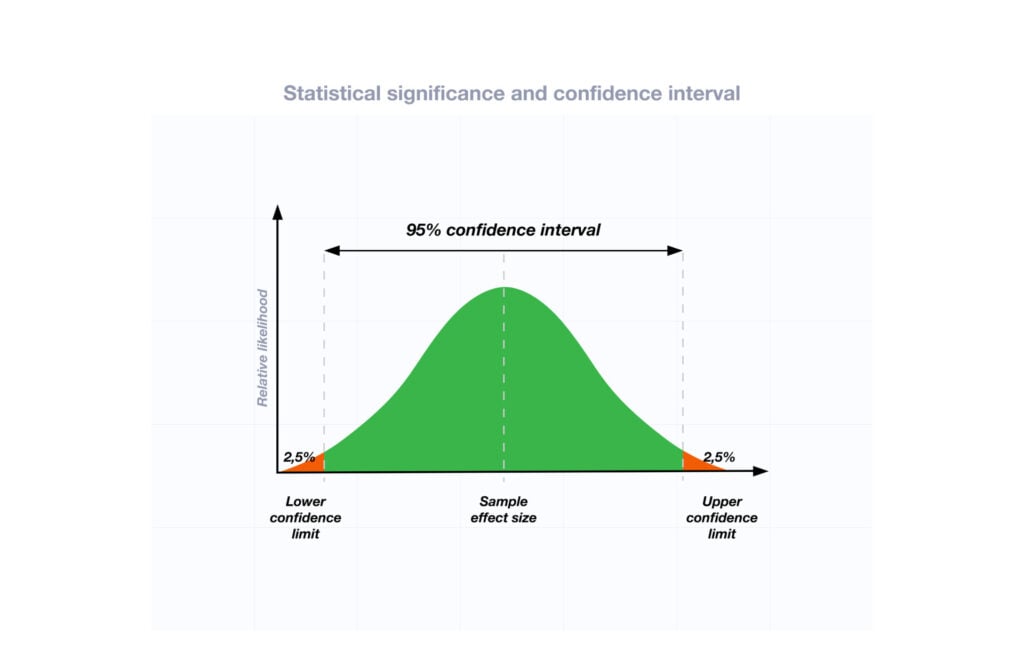
The significance (or alpha) level is the threshold we use to decide whether or not to reject the null hypothesis. Confidence intervals, on the other hand, are a range of values that contain the true population parameter. For example, a 95% confidence interval means 95% of the intervals would contain the true population parameter if a study were repeated many times.

Statistical significance and confidence levels are both related to the probability of making a Type I error. A Type I error—sometimes called a false-positive—is an error that occurs when a statistician rejects the null hypothesis when it is actually true. The probability of making a Type I error is equal to the significance level and is also the complement of the confidence level.

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Intro to Statistics

How data describes our world.

Intro to Microeconomics

Why small choices have big impact.

Intro to Macroeconomics

How money moves our world.

Intro to Psychology

The science of the mind.

Related Articles

Calculating Logarithmic Regression Step-By-Step

Learn about logarithmic regression and the steps to calculate it. We’ll also break down what a logarithmic function is, why it’s useful, and a few examples.

Regression Coefficients: How To Calculate Them

Learn what regression coefficients are, how to calculate the coefficients in a linear regression formula, and much more

What Is the Interquartile Range (IQR)?

Learn what the interquartile range is, why it’s used in Statistics and how to calculate it. Also read about how it can be helpful for finding outliers.

Further Reading

Discrete & continuous variables with examples, coefficient regression: definition, formula, and examples, what is statistics, degrees of freedom in statistics, understanding the pearson correlation coefficient.

• Search Search Please fill out this field.

What Is Statistical Significance?

Understanding statistical significance.

• Statistical Significance FAQs

The Bottom Line

• Corporate Finance
• Financial Analysis

Statistical Significance: What It Is, How It Works, With Examples

Statistical significance is a determination made by an analyst that the results in data aren't explainable by chance alone. Statistical  hypothesis testing  is the method by which the analyst makes this determination. The test provides a p-value , which is the probability of observing results as extreme as those in the data assuming the results are truly due to chance alone.

A p-value of 5% or lower is often considered to be statistically significant.

Key Takeaways

• Statistical significance is a determination that a relationship between two or more variables is caused by something other than chance.
• It's used to provide evidence concerning the plausibility of the null hypothesis that hypothesizes that there's nothing more than random chance at work in the data.
• Statistical hypothesis testing is used to determine whether the result of a data set is statistically significant.
• A p-value of 5% or lower is generally considered statistically significant.

Investopedia / Paige McLaughlin

Statistical significance is a determination of the  null hypothesis which suggests that the results are due to chance alone. A data set provides statistical significance when the p-value is sufficiently small.

The results in the data are explainable by chance alone when the p-value is large and the data are deemed consistent with the null hypothesis although they don't prove it.

The results aren't easily explained by chance alone when the p-value is sufficiently small, typically 5% or less, and the data are deemed inconsistent with the null hypothesis. The null hypothesis of chance alone is rejected as an explanation of the data in favor of a more systematic explanation in this case.

Statistical significance is often used for new pharmaceutical drug trials, to test vaccines, and in the study of pathology for effectiveness testing. It can inform investors on how successful the company is at releasing new products .

Examples of Statistical Significance

Suppose Alex, a financial analyst, is curious as to whether some investors had advance knowledge of a company's sudden failure. Alex decides to compare the average of daily market returns before the company's failure with those after to see if there's a statistically significant difference between the two averages.

The study's p-value was 28% (>5%), indicating that a difference as large as the observed (-0.0033 to +0.0007) isn't unusual under the chance-only explanation. The data therefore didn't provide compelling evidence of advance knowledge of the failure.

The observed difference would be very unusual under the chance-only explanation if the p-value was 0.01%, much less than 5%. Alex might decide to reject the null hypothesis in this case and further investigate whether some traders had advance knowledge

Statistical significance is also used to test new medical products including drugs, devices, and vaccines. Publicly available reports of statistical significance also inform investors about how successful the company is at releasing new products.

Suppose a pharmaceutical leader in diabetes medication reported that there was a statistically significant reduction in diabetes when it tested its new insulin. The test consisted of 26 weeks of randomized therapy among diabetes patients and the data gave a p-value of 4%. This signifies to investors and regulatory agencies that the data show a statistically significant reduction in diabetes.

Stock prices of pharmaceutical companies are often affected by announcements of the statistical significance of their new products.

How Is Statistical Significance Determined?

Statistical hypothesis testing is used to determine whether data is statistically significant and whether a phenomenon can be explained as a byproduct of chance alone. Statistical significance is a determination of the null hypothesis which posits that the results are due to chance alone. The rejection of the null hypothesis is necessary for the data to be deemed statistically significant.

What Is P-Value?

A p-value is a measure of the probability that an observed difference could have occurred just by random chance. The results are not easily explained by chance alone and the null hypothesis can be rejected when the p-value is sufficiently small, 5% or less. The results in the data are explainable by chance alone and the data is deemed consistent, proving the null hypothesis when the p-value is large.

How Is Statistical Significance Used?

Statistical significance is often used to test the effectiveness of new medical products, including drugs, devices, and vaccines. Publicly available reports of statistical significance also inform investors as to how successful the company is at releasing new products. Stock prices of pharmaceutical companies are often affected strongly by announcements of the statistical significance of their new products.

Statistical significance is a result of hypothesis testing that arrives at a p-value or likelihood that two or more variables are caused by something other than chance. A 5% p-value tends to be the dividing line. The lower the value, the more statistically significant the result of the data set is considered to be.

This form of testing is frequently used to assess pharmaceutical drug trials but it can be helpful for investors as well, particularly those who want to assess a company that’s releasing a new product.

Tenny, Steven and Abdelgawad, Ibrahim. " Statistical Significance. " StatPearls Publishing, 2023.

American Diabetes Association. " Efficacy and Safety of Fast-Acting Aspart Compared With Insulin Aspart, Both in Combination With Insulin Degludec, in Children and Adolescents With Type 1 Diabetes: The Onset 7 Trial ."

Hwang, Thomas J. " Stock Market Returns and Clinical Trial Results of Investigational Compounds: An Event Study Analysis of Large Biopharmaceutical Companies. " PLOS ONE, 2013.

Rothenstein, Jeffrey, et al. " Company Stock Prices Before and After Public Announcements Related to Oncology Drugs. " Journal of the National Cancer Institute , vol. 103, no. 20, October 2011, pp. 1507-1512.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

• How it works

"Christmas Offer"

Terms & conditions.

As the Christmas season is upon us, we find ourselves reflecting on the past year and those who we have helped to shape their future. It’s been quite a year for us all! The end of the year brings no greater joy than the opportunity to express to you Christmas greetings and good wishes.

At this special time of year, Research Prospect brings joyful discount of 10% on all its services. May your Christmas and New Year be filled with joy.

We are looking back with appreciation for your loyalty and looking forward to moving into the New Year together.

"Claim this offer"

In unfamiliar and hard times, we have stuck by you. This Christmas, Research Prospect brings you all the joy with exciting discount of 10% on all its services.

Offer valid till 5-1-2024

We love being your partner in success. We know you have been working hard lately, take a break this holiday season to spend time with your loved ones while we make sure you succeed in your academics

Discount code: RP0996Y

Statistical Significance: A Thorough Guide

Published by Jamie Walker at August 25th, 2021 , Revised On August 3, 2023

When running an experiment, you might come across this term significant times, so we thought of comprising all the information you need to know about it. This blog sheds light on what it means for a result to be statistically significant and how to check that in research; let’s begin then.

What is Statistical Significance?

Statistical significance is described as the measure of the null hypothesis being plausible as compared to the acceptable level of vagueness regarding the true answer.

A null hypothesis , which you may remember, is a statistical theory suggesting that there exists no relationship in a set of variables.

In other words, the result of an experiment is considered to be statistically significant if it is not caused by chance for a given statistical significance level. The statistically significant level shows the risk tolerance and confidence level.

Now, what are both these terms?

The significance level in hypothesis testing is the probability or chance of making the wrong decision when the null hypothesis is plausible. It is denoted by the letter alpha.

While the confidence level is the probability that if a particular test or survey is repeated several times, the correct results can be obtained, it is denoted by 1-alpha.

If you conduct an A/B testing experiment with a significance level of, say, 95 per cent. It means that if you select a winner, you can be 95 per cent confident that the obtained outcomes are not an error caused by uncertainty. You can also say that there are 5 per cent chances of you being wrong.

Does this all make sense to you now?

Good! Let’s move forward, then.

Testing for Statistical Significance

When it comes to quantitative research , data can be assessed and evaluated via hypothesis testing or null hypothesis significance testing. This is a formal process for analyzing whether there is a statistically significant relationship between the variables or not.

Let’s recall null and alternative hypotheses before digging deeper.

• What is a null hypothesis?

A null hypothesis says there is no relationship between variables. It is denoted by H 0 .

• What is an alternative hypothesis?

This one predicts that there is an effect or relationship between variables. An alternative hypothesis is shown by the sign H a  or H 1.

Hypothesis testing always begins by assuming that the null hypothesis is plausible or true. With this method, you can evaluate and analyze the probability of getting your results under this prediction or assumption. Once done, you can either retain or reject the null hypothesis based on the results.

A statistically significant outcome not happening by chance depends on two key factors or variables:

Sample Size:

This refers to how small or big your sample is for a particular experiment. If the sample size is big, you can be more confident in the outcome of the study.

Effect Size:

Effect size is the size difference in results between the sample sets. If the effect size is small, you might need a huge sample size to check whether the difference is due to chance or is actually significant. On the contrary, if you observe a larger effect, you can validate it with a smaller sample size to a greater degree of confidence.

P values and Test Statistics

Two things are always produced by every statistical test :

• P-value – it tells you the chances of obtaining this result if the null hypothesis is plausible
• Test statistic -it indicates how close your data is related to the null hypothesis

Get statistical analysis help at an affordable price

• An expert statistician will complete your work
• Rigorous quality checks
• Confidentiality and reliability
• Any statistical software of your choice
• Free Plagiarism Report

Why is Statistical Significance Significant in Research?

Statistical significance is of great value because it gives researchers a chance to confirm whether the findings they have at hand are reliable, real, and not something that occurred due to probability. However, the importance of statistical significance varies from researcher to researcher and the experiment they work on. The context in which a particular experiment is also conducted directly impacts the impact of statistical significance.

Statistical significance is crucial within academic research. It is mostly utilized in new pharmaceutical drug trials along with pathology studies in order to check vaccines. Moreover, the aim and objectives of academic research are to study and publish a series of scientific journals for which you need to make sure the results are statistically significant.

Outside of science and academics, statistical significance is, however, less important. Managers and business persons might use this to better comprehend and evaluate business strategies, but the fact that statistical significance is just quantifying how much trust to hold in research, people are least interested in this industry. They are undoubtedly more curious about the practical significance of a finding instead of statistical significance.

And this brings us to what practical significance is and how it is different from statistical significance.

Practical significance describes whether the research finding is significant enough to be meaningful in the actual world. It is shown by the effect size of the experiment or study.

So, the difference between these two is that statistical significance predicts that an effect exists in a study, while practical significance shows that the result is so big that it does not hold any impact in the real world.

This is all for this blog. If you have questions and requests, please feel free to contact our experts.

FAQs about Statistical Significance

1. what is statistical significance.

Statistical significance is described as the measure of the null hypothesis being plausible as compared to the acceptable level of uncertainty regarding the true answer. In other words, the result of an experiment is considered to be statistically significant if it is not caused by chance for a given statistical significance level. The statistically significant level shows the risk tolerance and confidence level.

2. What is the p-value?

The p-value tells you the chances of obtaining this result if the null hypothesis is plausible

3. What is a test statistic?

Test statistic indicates how close your data is related to the null hypothesis

4. Differentiate between statistical significance and practical significance.

The difference between these two is that statistical significance predicts that an effect exists in a study, while practical significance shows that the result is so big that it does not hold any impact in the real world.

5. What is the significance level?

6. what is the null and alternative hypothesis.

A null hypothesis says there is no relationship between variables. It is denoted by H0. An alternative hypothesis predicts that there is an effect or relationship between variables. It is showed by the sign Ha or H1.

You May Also Like

Measures of variability in statistics is a summary explaining the proportions of fluctuation in the dataset.

Experimental research refers to the experiments conducted in the laboratory or under observation in controlled conditions. Here is all you need to know about experimental research.

A dependent variable is one that completely depends on another variable, mostly the independent one.

As Featured On

USEFUL LINKS

LEARNING RESOURCES

COMPANY DETAILS

Splash Sol LLC

• How It Works