Assignment Problem: Meaning, Methods and Variations | Operations Research
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Definition of Assignment Problem:
ADVERTISEMENTS:
Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:
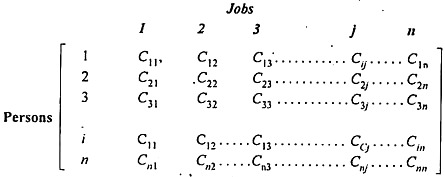
x ij is missing in any cell means that no assignment is made between the pair of job and machine.( i.e ) x ij = 0.
x ij presents in any cell means that an assignment is made their.In such cases x ij = 1
The assignment model can be written in LPP as follows
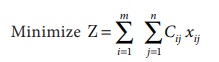
Subject to the constrains
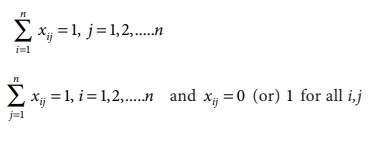
The optimum assignment schedule remains unaltered if we add or subtract a constant from all the elements of the row or column of the assignment cost matrix.
If for an assignment problem all C ij > 0 then an assignment schedule (x ij ) which satisfies ∑ C ij x ij = 0 must be optimal.
Related Topics
Privacy Policy , Terms and Conditions , DMCA Policy and Compliant
Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.
- Practice Mathematical Algorithm
- Mathematical Algorithms
- Pythagorean Triplet
- Fibonacci Number
- Euclidean Algorithm
- LCM of Array
- GCD of Array
- Binomial Coefficient
- Catalan Numbers
- Sieve of Eratosthenes
- Euler Totient Function
- Modular Exponentiation
- Modular Multiplicative Inverse
- Stein's Algorithm
- Juggler Sequence
- Chinese Remainder Theorem
- Quiz on Fibonacci Numbers
Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Do the same (as step 1) for all columns.
- Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
- Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Try it before moving to see the solution
Explanation for above simple example:
An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.
Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).
Space complexity : O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.
In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY
Similar Reads
- Mathematical
Improve your Coding Skills with Practice
What kind of Experience do you want to share?

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.
Hungarian Method to Solve Assignment Problems
The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.
What is an Assignment Problem?
A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.
Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.
Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.
Hungarian Method Steps
Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.
Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.
Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.
Step 3 – Assign zeros
- Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
- Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.
Step 4 – Perform the Optimal Test
- The present assignment is optimal if each row and column has exactly one encircled zero.
- The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.
Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:
(a) Highlight the rows that aren’t assigned.
(b) Label the columns with zeros in marked rows (if they haven’t already been marked).
(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).
(d) Continue with (b) and (c) until no further marking is needed.
(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.
Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.
Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.
Hungarian Method Example
Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.
\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
With 5 jobs and 5 men, the stated problem is balanced.
\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)
Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)
When the zeros are assigned, we get the following:
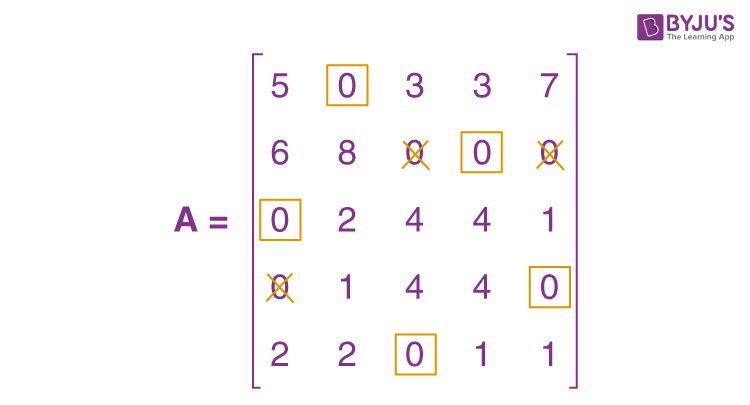
The present assignment is optimal because each row and column contain precisely one encircled zero.
Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.
Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.
Practice Question on Hungarian Method
Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.
\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.
Frequently Asked Questions on Hungarian Method
What is hungarian method.
The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.
What are the steps involved in Hungarian method?
The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.
What is the purpose of the Hungarian method?
When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

COMMENTS
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment.
In applied mathematics, the maximum generalized assignment problem is a problem in combinatorial optimization. This problem is a generalization of the assignment problem in which both tasks and agents have a size. Moreover, the size of each task might vary from one agent to the other. This problem in its most general form is as follows: There ...
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total ...
The optimum assignment schedule remains unaltered if we add or subtract a constant from all the elements of the row or column of the assignment cost matrix. Note. If for an assignment problem all Cij > 0 then an assignment schedule (xij) which satisfies ∑ Cij xij = 0 must be optimal. Consider the problem of assigning n jobs to n machines (one ...
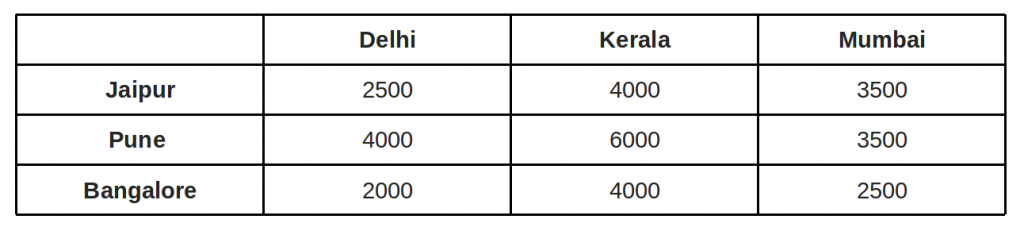
Step 3: Cover all zeroes with minimum number of. horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, we have found the optimal assignment. 2500 4000 3500. 4000 6000 3500. 2000 4000 2500. So the optimal cost is 4000 + 3500 + 2000 = 9500. An example that doesn’t lead to optimal value in first attempt: In the above ...
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry.
Hungarian method for assignment problem Step 1. Subtract the entries of each row by the row minimum. Step 2. Subtract the entries of each column by the column minimum. Step 3. Make an assignment to the zero entries in the resulting matrix. A = M 17 10 15 17 18 M 6 10 20 12 5 M 14 19 12 11 15 M 7 16 21 18 6 M −10
5.5.1 General Form and Assumptions The general assignment problem involves the assignment of n resources (origins) to n tasks (destinations). The objective in making assignments can be one of minimization or minimization (e.g minimization of total time required to complete n tasks or maximization of total profits from
The problem dual to the General Assignment Problem is then: What is the smallest total allotment ul+. . . + Un+V1 +. , . + 'n possible for an adequate budget? The following analogue of Theorem 3 is immediate. THEOREM 5. The total allotment of any adequate budget is not less than the rating sum of any assignment. PROOF.
UNIT -2. r: IIASSIGNMENT PROBLEMIntroduction:Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a. number of jobs by a number of persons. The assignment problem in the general form can be stated as follows: “Given n facilities, n jobs and the effectiveness of ...